题目内容
已知a、b为有理数，则多项式a2+b2-2a-6b+12的值为（ ）
| A、正数 | B、零 | C、负数 | D、非负数 |
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：将多项式a2+b2-2a-6b+12配方后即可确定题目的答案．
解答：解：a2+b2-2a-6b+12=a2-2a+1+b2-6b+9+2=（a-1）2+（b-3）2+2，
∵（a-1）2≥0，（b-3）2≥0，
∴a2+b2-2a-6b+12＞0，
故选A．
∵（a-1）2≥0，（b-3）2≥0，
∴a2+b2-2a-6b+12＞0，
故选A．
点评：考查了配方法的应用及非负数的性质，解题的关键是将多项式进行正确的配方．
练习册系列答案
相关题目
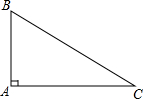如图，在△ABC中，AB⊥AC，垂足为A．
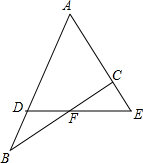如图所示，已知AD：DB=7：2，AC：CE=4：3，则BF：FC=
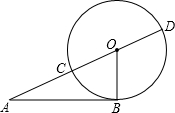如图，在Rt△ABO中，∠B=Rt∠，以O为圆心，OB为半径画圆，分别交AO和AO的延长线于C、D，若OB=1，AB=3；
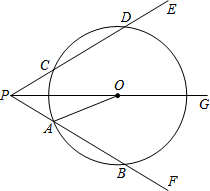如图，射线PG平分∠EPF，O为射线PG上一点，以O为圆心，10为半径作⊙O，分别与∠EPF两边相交于A、B和C、D，连结OA，此时有OA∥PE．