题目内容
4. 如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )| A. | y=-$\sqrt{3}$x2+6$\sqrt{3}$x-8$\sqrt{3}$ | B. | y=-2$\sqrt{3}$x2-12$\sqrt{3}$x+16$\sqrt{3}$ | ||
| C. | y=2$\sqrt{3}$x2+12$\sqrt{3}$x-16$\sqrt{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x2+2$\sqrt{3}$x-$\frac{8\sqrt{3}}{3}$ |
分析 由折叠性质可得AE=A′E=x、∠BEM=∠B′EM=60°、∠B=∠EB′M=90°、BE=B′E=4-x,继而可得BM=BM′=BEtan∠BEM=$\sqrt{3}$(4-x)、A′B′=A′E-B′E=2x-4,根据三角形面积公式即可得.
解答 解:∵∠AEF=60°,
∴∠BEF=120°,
由题意知,∠BEM=∠B′EM=60°,∠B=∠EB′M=90°,BE=B′E=4-x,
∴BM=BM′=BEtan∠BEM=$\sqrt{3}$(4-x),
又∵AE=A′E=x,
∴A′B′=A′E-B′E=x-(4-x)=2x-4,
∵S△A′B′M=$\frac{1}{2}$×A′B′×B′M,
∴y=$\frac{1}{2}$(2x-4)[$\sqrt{3}$(4-x)]=-$\sqrt{3}$x2+6$\sqrt{3}$x-8$\sqrt{3}$,
故选:A.
点评 本题主要考查根据实际问题列二次函数解析式,熟练掌握折叠前后对应边相等、对应角相等的性质是解题的关键.

练习册系列答案
相关题目
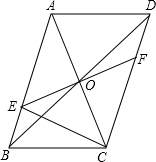 如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
如图,?ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC. 如图是由10个相同的小长方形拼成的长方形图案,则每块小长方形的面积为400cm2.
如图是由10个相同的小长方形拼成的长方形图案,则每块小长方形的面积为400cm2. 如图,在⊙O中,弦CD垂直于直径AB,垂足为H,CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )
如图,在⊙O中,弦CD垂直于直径AB,垂足为H,CD=2$\sqrt{2}$,BD=$\sqrt{3}$,则AB的长为( )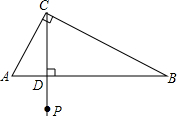 如图,在△ABC中,∠ACB=90°,∠B=30°,BC=6,CD为AB边上的高,点P为射线CD上一动点,当点P运动到使△ABP为等腰三角形时,BP的长度为4$\sqrt{3}$或6$\sqrt{2}$.
如图,在△ABC中,∠ACB=90°,∠B=30°,BC=6,CD为AB边上的高,点P为射线CD上一动点,当点P运动到使△ABP为等腰三角形时,BP的长度为4$\sqrt{3}$或6$\sqrt{2}$. 如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.
如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.