题目内容
16. 如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.
如图,已知点A、B、C是⊙O上的点,其中点C是弧AB的中点,OC=4cm,点P是OC延长线上一点,连接PA、PB.(1)求证:PA=PB;
(2)填空:
①若∠BOA=90°,当PB=4cm时,四边形OAPB是正方形;
②若∠BOA=120°,当OP=4cm时,四边形OAPB是菱形.
分析 (1)由弧的中点,得到∠BOC=∠AOC,用SAS直接判断出△BOP≌△AOP,即可;
(2)①由正方形的性质得到PB=OB即可;
②由菱形的性质得到BP=OB,再由∠BOA=120°,判断出△BOP是等边三角形即可.
解答 解:(1)∵点C是弧AB的中点,
∴∠BOC=∠AOC,
在△BOP和△AOP中$\left\{\begin{array}{l}{OA=OB}\\{∠AOP=∠BOP}\\{OP=OP}\end{array}\right.$,
∴△BOP≌△AOP,
∴PA=PB,
(2)①∵OC=4,
∴OB=OC=4
∵四边形OAPB是正方形,且∠BOA=90°,
∴OB=PB=4cm,
故答案为4,
②由(1)得,∠BOP=∠AOP=$\frac{1}{2}$∠BOA=60°
∵四边形OAPB是菱形,
∴OB=BP,
∴△BOP是等边三角形,
∴OP=OB=4cm
故答案为4.
点评 此题是圆的综合题,主要考查了圆的性质,全等三角形的判定和性质,正方形的性质,菱形的性质,解本题的关键是判断出△BOP≌△AOP.

练习册系列答案
相关题目
4. 如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )
 如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )
如图,矩形ABCD中,AB=4,AD=3,点E、F分别在边AB,CD上,且∠FEA=60°,连接EF,将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN,当M,N分别在边BC,AD上时.若令△A′B′M的面积为y,AE的长度为x,则y关于x的函数解析式是( )| A. | y=-$\sqrt{3}$x2+6$\sqrt{3}$x-8$\sqrt{3}$ | B. | y=-2$\sqrt{3}$x2-12$\sqrt{3}$x+16$\sqrt{3}$ | ||
| C. | y=2$\sqrt{3}$x2+12$\sqrt{3}$x-16$\sqrt{3}$ | D. | y=-$\frac{\sqrt{3}}{3}$x2+2$\sqrt{3}$x-$\frac{8\sqrt{3}}{3}$ |
6. 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是( )
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是( )
 如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是( )
如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是( )| A. | 2 | B. | 2$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{3}$ |

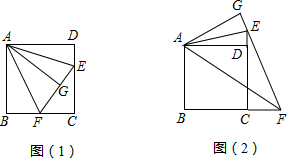
 正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.
正方形ABCD和正方形CEFG,连结BF,DF,点P为线段DF的中点,连接GP.