题目内容
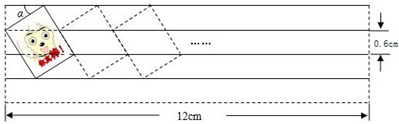
如图,现有一张宽为12cm练习纸,相邻两条格线间的距离均为0.6cm.调皮的小聪在纸的左上角用印章印出一个矩形卡通图案,图案的顶点恰好在四条格线上,已知sinα=
.
(1)求一个矩形卡通图案的面积;
(2)若小聪在第一个图案的右边以同样的方式继续盖印,最多能印几个完整的图案?
| 3 |
| 5 |
(1)求一个矩形卡通图案的面积;
(2)若小聪在第一个图案的右边以同样的方式继续盖印,最多能印几个完整的图案?

考点:解直角三角形的应用
专题:
分析:(1)如图,在Rt△BCE中,由sinα=
可以求出BC,在矩形ABCD中由∠BCD=90°得到∠BCE+∠FCD=90°,又在Rt△BCE中,利用已知求出条件∠FCD=∠CBE,然后在Rt△FCD中,由cos∠FCD=
求出CD,因此求出了矩形图案的长和宽;求得面积;
(2)如图,在Rt△ADH中,易求得∠DAH=∠CBE.由cos∠DAH=
,求出AH,在Rt△CGH中,由tan∠GCH=
求出GH,最后即可确定最多能摆放多少块矩形图案,即最多能印几个完整的图案.
| CE |
| BC |
| FC |
| CD |
(2)如图,在Rt△ADH中,易求得∠DAH=∠CBE.由cos∠DAH=
| AD |
| AH |
| GH |
| CG |
解答:解:(1)如图,在Rt△BCE中,
∵sinα=
,
∴BC=
=
=1
∵矩形ABCD中,
∴∠BCD=90°,
∴∠BCE+∠FCD=90°,
又∵在Rt△BCE中,
∴∠EBC+∠BCE=90°,
∴∠FCD=∠CBE.
在Rt△FCD中,
∵cos∠FCD=
,
∴CD=
=1.5
∴卡通图案的面积为1.5cm2.
(2)如图,在Rt△ADH中,易求得∠DAH=∠CBE.
∵cos∠DAH=
,

∴AH=
=1.25
在Rt△CGH中,∠GCH=∠CBE.
∵tan∠GCH=
,
∴GH=0.45
又∵10×1.25+0.45>12,9×1.25+0.45<12,
∴最多能印9个完整的图案.
∵sinα=
| CE |
| BC |
∴BC=
| CE |
| sinα |
| 0.6 |
| 0.6 |
∵矩形ABCD中,
∴∠BCD=90°,
∴∠BCE+∠FCD=90°,
又∵在Rt△BCE中,
∴∠EBC+∠BCE=90°,
∴∠FCD=∠CBE.
在Rt△FCD中,
∵cos∠FCD=
| FC |
| CD |
∴CD=
| 1.2 |
| 0.8 |
∴卡通图案的面积为1.5cm2.
(2)如图,在Rt△ADH中,易求得∠DAH=∠CBE.
∵cos∠DAH=
| AD |
| AH |

∴AH=
| 1 |
| 0.8 |
在Rt△CGH中,∠GCH=∠CBE.
∵tan∠GCH=
| GH |
| CG |
∴GH=0.45
又∵10×1.25+0.45>12,9×1.25+0.45<12,
∴最多能印9个完整的图案.
点评:此题主要考查矩形的性质、解直角三角形等知识,难度较大,是一个综合性很强的题目,有利于培养同学们钻研和探索问题的精神.

练习册系列答案
相关题目

 若反比例函数y1=
若反比例函数y1=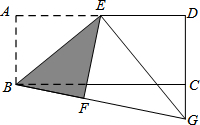 如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.
如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G. 如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2).
如图,在平面直角坐标系中,△ABC的顶点A的坐标是(-3,2). 如图,在△ABC中,AD⊥BC,垂足为D.
如图,在△ABC中,AD⊥BC,垂足为D. 在边长为1的小正方形组成的网格中,有如图的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为
在边长为1的小正方形组成的网格中,有如图的A,B两点,在格点上任意放置点C,恰好能使得△ABC的面积为1的概率为