题目内容
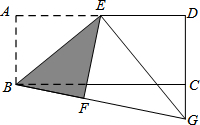 如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.
如图,在矩形ABCD中,E是AD的中点,把矩形沿BE折叠,使点A落在矩形外的一点F上,连接BF并延长交DC的延长线于点G.(1)求证:△EFG≌△EDG.
(2)当DG=3,BC=2
| 6 |
考点:翻折变换(折叠问题)
专题:
分析:(1)根据折叠的性质和矩形的性质可得△EFG与△EDG是直角三角形,DE=AE=FE,再根据HL即可证明△EFG≌△EDG.
(2)根据全等三角形的性质可得DG=FG=3,在Rt△BCG中,根据勾股定理可求CG的长.
(2)根据全等三角形的性质可得DG=FG=3,在Rt△BCG中,根据勾股定理可求CG的长.
解答:(1)证明:E是边AD的中点,
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°
∴∠D=∠EFG=90°.
在Rt△EFG与Rt△EDG中,
,
∴Rt△EFG≌Rt△EDG(HL);
(2)解:∵△EFG≌△EDG,
∴DG=FG=3,
设CG=x,DC=3-x,
AB=BF=DC=3-x
BG=3-x+3=6-x
在Rt△BCG中,
BG2=BC2+CG2,
(6-x)2=(2
)2+x2,
解得x=1,
即CG=1.
∴DE=AE=FE,
又∵四边形ABCD是矩形,
∴∠D=∠A=∠BFE=90°
∴∠D=∠EFG=90°.
在Rt△EFG与Rt△EDG中,
|
∴Rt△EFG≌Rt△EDG(HL);
(2)解:∵△EFG≌△EDG,
∴DG=FG=3,
设CG=x,DC=3-x,
AB=BF=DC=3-x
BG=3-x+3=6-x
在Rt△BCG中,
BG2=BC2+CG2,
(6-x)2=(2
| 6 |
解得x=1,
即CG=1.
点评:考查了翻折变换(折叠问题),涉及的知识点有:折叠的性质,矩形的性质,全等三角形的判定和性质以及勾股定理,综合性较强,有一定的难度.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
 如图,已知直角三角形ABC,∠C=90°.
如图,已知直角三角形ABC,∠C=90°.

 钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.
钓鱼岛及其附属daoyu是我国的固有领土,台湾保diao人士组团前往钓鱼岛,宣示主权.当保diao船航行至海面B处时(如图),测得钓鱼岛位于正北方向20海里的C处,为了防止日本海巡警干扰,就请求我A处的海监船前往C处护航.已知C处位于A处的北偏东45°的方向上,A位于B的北偏西30°的方向上.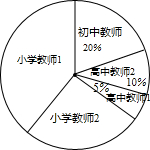 萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)
萧山区2014教师招聘有拉开序幕,这给很多有志于教育事业的人员很多机会.下面是今年报考人数统计表(数学)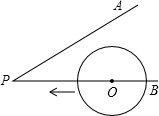 如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为
如图,∠APB=30°,点O是射线PB上的一点,OP=5cm,若以点O为圆心,半径为1.5cm的⊙O沿BP方向移动,当⊙O与PA相切时,圆心O移动的距离为