题目内容
如图，在△ABC中，AD⊥BC，垂足为D．（1）尺规作图（不写作法，保留作图痕迹）：作△ABC的外接圆⊙O，作直径AE，连接BE；
（2）若AB=10，AC=8，AD=6，求BE的长．
考点：作图—复杂作图,三角形的外接圆与外心
专题：
分析：（1）首先利用三角形外接圆的作法得出AB，BC的垂直平分线，进而得出圆心位置，进而得出符合题意的图形；
（2）利用三角形相似的判定与性质得出
=
，进而求出即可．
（2）利用三角形相似的判定与性质得出
| AB |
| AD |
| BE |
| DC |
解答：
解：（1）如图所示：
（2）∵AE是⊙O直径，
∴∠ABE=90°，
∵∠C=∠E，∠ADC=∠ABE，
∴△ABE∽△ADC，
∴
=
，
∵AD=6，AC=8，
∴DC=2
，
∴
=
，
解得：BE=
．
解：（1）如图所示：（2）∵AE是⊙O直径，
∴∠ABE=90°，
∵∠C=∠E，∠ADC=∠ABE，
∴△ABE∽△ADC，
∴
| AB |
| AD |
| BE |
| DC |
∵AD=6，AC=8，
∴DC=2
| 7 |
∴
| 10 |
| 6 |
| BE | ||
2
|
解得：BE=
10
| ||
| 3 |
点评：此题主要考查了三角形的外接圆的作法以及相似三角形的判定与性质等知识，得出DC的长进而求出是解题关键．
练习册系列答案
相关题目
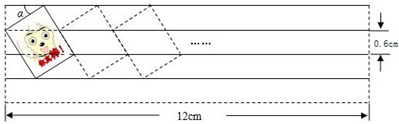
钓鱼岛及其附属daoyu是我国的固有领土，台湾保diao人士组团前往钓鱼岛，宣示主权．当保diao船航行至海面B处时（如图），测得钓鱼岛位于正北方向20海里的C处，为了防止日本海巡警干扰，就请求我A处的海监船前往C处护航．已知C处位于A处的北偏东45°的方向上，A位于B的北偏西30°的方向上．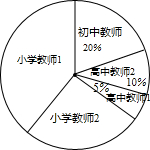
萧山区2014教师招聘有拉开序幕，这给很多有志于教育事业的人员很多机会．下面是今年报考人数统计表（数学）