题目内容
14.已知△ABC中,AB=4,AC=8,点D是BC的中点,则AD的取值范围是2<AD<6.分析 作出图形,延长AD至E,使DE=AD,根据三角形中线的定义可得BD=CD,然后利用“边角边”证明△ABD和△ECD全等,根据全等三角形对应边相等可得CE=AB,再根据三角形的任意两边之和大于第三边,任意两边只差小于第三边求出AE,然后求解即可.
解答 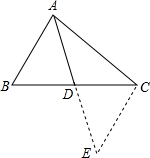 解:如图,延长AD至E,使DE=AD,
解:如图,延长AD至E,使DE=AD,
∵AD是△ABC中BC边上的中线,
∴BD=CD,
在△ABD和△ECD中,
$\left\{\begin{array}{l}{AD=DE}\\{∠ADB=∠EDC}\\{BD=CD}\end{array}\right.$,
∴△ABD≌△ECD(SAS),
∴CE=AB=4,
∵AC=8,
∴4+8=112,8-4=4,
∴4<AE<12,
∴2<AD<6.
故答案为:2<AD<6.
点评 本题考查了全等三角形的判定与性质,三角形的三边关系,“遇中线,加倍延”构造出全等三角形是解题的关键,作出图形更形象直观.

练习册系列答案
相关题目
14. 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | ∠2与∠1是同位角 | B. | ∠C与∠1是内错角 | ||
| C. | ∠2与∠3是同旁内角 | D. | ∠B与∠3是同位角 |
15.下列命题的逆命题不正确的是( )
| A. | 同旁内角互补,两直线平行 | |
| B. | 如果两个角是直角,那么它们相等 | |
| C. | 两个全等三角形的对应边相等 | |
| D. | 如果两个实数的平方相等,那么它们相等 |
19.已知P=$\frac{7}{17}$m-1,Q=m2-$\frac{10}{17}$m(m为任意实数),则P与Q的大小关系为( )
| A. | P>Q | B. | P=Q | C. | P<Q | D. | 不能确定 |
6.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,当种植樱桃的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系如表(为所学过的一次函数,反比例函数或二次函数中的一种).
(1)请求出每亩获得利润y与x的函数关系式,并写出自变量的取值范围;
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过60亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
| x(亩) | 20 | 25 | 30 | 35 |
| y(元) | 1800 | 1700 | 1600 | 1500 |
(2)如果小王家计划承包荒山种植樱桃,受条件限制种植樱桃面积x不超过60亩,设小王家种植x亩樱桃所获得的总利润为W元,求小王家承包多少亩荒山获得的总利润最大,并求总利润W(元)的最大值.
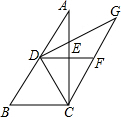 如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F.
如图,在△ABC中,∠ACB=90°,∠B>∠A,AE=EC,∠A=∠DCA,CF∥AB交DE的延长线于点F. 如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )
如图,过△ABC的顶点A,作BC边上的高,以下作法正确的是( )



 如图,正方形ABCD中,E、F分别是BC、CD的中点,连结AE、BF交于点H.试判断AE与BF的数量关系和位置关系,并证明你的结论.
如图,正方形ABCD中,E、F分别是BC、CD的中点,连结AE、BF交于点H.试判断AE与BF的数量关系和位置关系,并证明你的结论.