题目内容
4. 如图,正方形ABCD中,E、F分别是BC、CD的中点,连结AE、BF交于点H.试判断AE与BF的数量关系和位置关系,并证明你的结论.
如图,正方形ABCD中,E、F分别是BC、CD的中点,连结AE、BF交于点H.试判断AE与BF的数量关系和位置关系,并证明你的结论.
分析 AE=BF,AE⊥BF,首先证△ABE≌△BCF,推出AE=BF,∠BAE=∠CBF,求出∠CBF+∠AEB=90°,求出∠BHE=90°即可.
解答 解:AE=BF,AE⊥BF,理由如下:
∵四边形ABCD是正方形,
∴∠ABE=∠C=90°,AB=BC,
∵在△ABE和△BCF中
$\left\{\begin{array}{l}{AB=BC}\\{∠ABE=∠C}\\{BE=CF}\end{array}\right.$,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵∠ABE=90°,
∴∠BAE+∠AEB=90°,
∴∠CBF+∠AEB=90°,
∴∠BHE=180°-90°=90°,
∴AE⊥BF.
点评 本题考查了正方形的性质以及全等三角形的判断和性质,熟记正方形的各种性质以及全等三角形的各种判断方法是解题的关键.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | a+2a=3a2 | B. | (-a)3=a3 | C. | a3÷a=3 | D. | a2•a3=a5 |
19. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
 如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )
如图是一个正方体的表面展开图,则原正方体中与“建”字所在面相对的面上的字是( )| A. | 美 | B. | 丽 | C. | 资 | D. | 中 |
9.下列多项式能因式分解的是( )
| A. | m2+n | B. | m2-m+n | C. | m2-2mn+n2 | D. | m2-n |
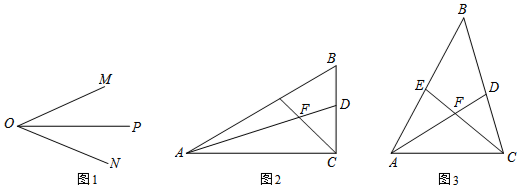
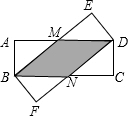 如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.
如图,已知四边形ABCD、四边形DEBF都是矩形,AB=BF,BE,AD交于点M,BC、DF交于点N,试说明四边形BMDN是菱形.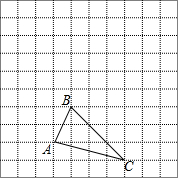 如图,已知单位长度为1的方格中有个△ABC,若A(-3,-3),B(-2,-1),C(0,-4).
如图,已知单位长度为1的方格中有个△ABC,若A(-3,-3),B(-2,-1),C(0,-4).