题目内容
9.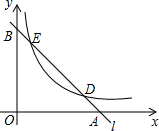 已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)
已知直线l分别与x轴、y轴交于A、B两点,与双曲线y=$\frac{m}{x}$(m≠0,x>0)分别交于D、E两点,若点D的坐标为(4,1),点E的坐标为(1,n)(1)分别求出直线l与双曲线的解析式;
(2)求△EOD的面积.
分析 (1)只需运用待定系数法就可求出反比例函数的解析式,把点E的坐标代入反比例函数的解析式,就可求出点E的坐标,然后运用待定系数法就可求出直线l的解析式;
(2)连接OD、OE,过点D作DM⊥OA于M,作EN⊥OA于N,如图,只需运用割补法,就可求出△EOD的面积.
解答 解:(1)把D(4,1)代入反比例函数的解析式得,
m=4×1=4,
∴反比例函数的解析式为y=$\frac{4}{x}$.
把点E(1,n)的坐标代入y=$\frac{4}{x}$得n=4,
∴点E的坐标为(1,4).
设直线l的解析式为y=kx+b,
则有$\left\{\begin{array}{l}{1=4k+b}\\{4=k+b}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴直线l的解析式为y=-x+5;
(2)连接OD、OE,过点D作DM⊥OA于M,作EN⊥OA于N,如图.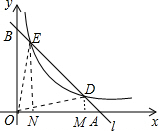
∵点A是直线y=-x+5与x轴的交点,
∴点A的坐标为(5,0),OA=5,
∴S△DOE=S△AOE-S△ADO
=$\frac{1}{2}$×5×4-$\frac{1}{2}$×5×1=$\frac{15}{2}$.
点评 本题主要考查了运用待定系数法求一次函数和反比例函数的解析式,运用割补法是解决第(2)小题的关键.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
 如图,已知AB∥CD,CN是∠BCE的平分线.
如图,已知AB∥CD,CN是∠BCE的平分线. 如图,在△ABC中点D、E分别在边AB、AC上,请添加一个条件:∠AEB=∠B(答案不唯一),使△ABC∽△AED.
如图,在△ABC中点D、E分别在边AB、AC上,请添加一个条件:∠AEB=∠B(答案不唯一),使△ABC∽△AED. 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$.
如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数y=$\frac{k}{x}$的图象经过点B,则k的值是$\sqrt{3}$. 如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.
如图,△ABC和△CEF均为等腰直角三角形,E在△ABC内,∠CAE+∠CBE=90°,连接BF.