题目内容
19.已知x2-3x+1=0,则$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2}$=( )| A. | 3 | B. | 4 | C. | $\sqrt{5}$ | D. | $\sqrt{7}$ |
分析 根据二次根式的性质,可化简二次根式,根据解方程,可得x的值,根据实数的运算,可得答案.
解答 解:x2-3x+1=0解得x=$\frac{3±\sqrt{5}}{2}$,
$\sqrt{{x}^{2}+\frac{1}{{x}^{2}}-2}$=$\sqrt{(x+\frac{1}{x})^{2}}$=|x+$\frac{1}{x}$|,
当x=$\frac{3+\sqrt{5}}{2}$时,原式=$\frac{3+\sqrt{5}}{2}$+$\frac{2}{3+\sqrt{5}}$=$\frac{6+2\sqrt{5}}{4}$+$\frac{6-2\sqrt{5}}{4}$=3,
当x=$\frac{3-\sqrt{5}}{2}$时,原式=$\frac{3-\sqrt{5}}{2}$+$\frac{2}{3-\sqrt{5}}$=$\frac{6-2\sqrt{5}}{4}$+$\frac{6+2\sqrt{5}}{4}$=3.
故选:A.
点评 本题考查了二次根式的性质与化简,利用二次根式的性质:$\sqrt{{a}^{2}}$=a (a≥0),分类讨论是解题关键,以防遗漏.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 用铁皮制作圆锥形状的容器盖如图所示,求这个容器盖铁皮的面积(结果保留π),并求制作容器盖的扇形的圆心角.
用铁皮制作圆锥形状的容器盖如图所示,求这个容器盖铁皮的面积(结果保留π),并求制作容器盖的扇形的圆心角. 如图,四边形ABCD三边切⊙O于F、G、H,说明AB+CD与BC+AD的大小关系.
如图,四边形ABCD三边切⊙O于F、G、H,说明AB+CD与BC+AD的大小关系.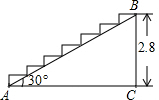 如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.
如图,某宾馆重新装修后,准备在大厅的主梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2米,其侧面如图所示(单位:米),求购买地毯至少需要多少元.