题目内容
18．计算3$\sqrt{3}$+$\sqrt{2}$-2$\sqrt{3}$=$\sqrt{2}+\sqrt{3}$，$\sqrt{x-2}$中x的取值范围是x≥2．分析 根据二次根式有意义的条件和加减法的法则计算即可．
解答 解：3$\sqrt{3}$+$\sqrt{2}$-2$\sqrt{3}$=$\sqrt{2}+\sqrt{3}$，
$\sqrt{x-2}$中x的取值范围是x≥2，
故答案为：$\sqrt{2}+\sqrt{3}$，x≥2．
点评 本题考查了二次根式有意义的条件和加减法的法则，熟记二次根式有意义的条件和加减法的法则是解题的关键．
练习册系列答案
相关题目
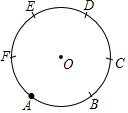尺规作图特有的魅力曾使无数人沉湎其中，连当年叱咤风云的拿破仑也不例外，我们可以只用圆规将圆等分．例如可将圆6等分，如图只需在⊙O上任取点A，从点A开始，以⊙O的半径为半径，在⊙O上依次截取点B，C，D，E，F．从而点A，B，C，D，E，F把⊙O六等分．下列可以只用圆规等分的是（ ）
6．下列计算正确的是（ ）
| A． | 3$\sqrt{3}$×5$\sqrt{3}$=15$\sqrt{3}$ | B． | 3$\sqrt{2}$$+2\sqrt{3}$=5$\sqrt{6}$ | C． | $\sqrt{8}$$-\sqrt{6}$=$\sqrt{2}$ | D． | $\sqrt{60}$$÷\sqrt{5}$=2$\sqrt{3}$ |
