题目内容
20.先化简,再求值:$\frac{x-2}{{x}^{2}-1}$•$\frac{x+1}{{x}^{2}-4x+4}$+$\frac{1}{x-1}$,从-1,0,1三个数中选一个合适的,代入求值.分析 先化简题目中的式子,然后将x=0代入化简后的式子即可解答本题.
解答 解:$\frac{x-2}{{x}^{2}-1}$•$\frac{x+1}{{x}^{2}-4x+4}$+$\frac{1}{x-1}$
=$\frac{x-2}{(x+1)(x-1)}•\frac{x+1}{{{{(x-2)}^2}}}+\frac{1}{x-1}$
=$\frac{1}{(x-1)(x-2)}+\frac{1}{x-1}$
=$\frac{1}{(x-1)(x-2)}+\frac{x-2}{(x-1)(x-2)}$
=$\frac{1}{x-2}$,
当x=0时,原式=$\frac{1}{x-2}=\frac{1}{0-2}=-\frac{1}{2}$.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法,注意x不能等于-1,1,2.

练习册系列答案
相关题目
15.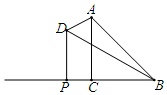 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
 如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )
如图,已知等腰直角三角形ABC中,∠ACB=90°,BC=1,在BC的延长线上任取一点P,过点P作PD⊥BC,使得PD=2PC,则当点P在BC延长线上向左移动时,△ABD的面积大小变化情况是( )| A. | 一直变大 | B. | 一直变小 | C. | 先变小再变大 | D. | 先变大再变小 |
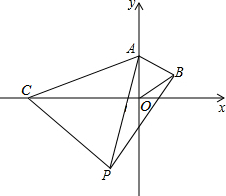 如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.
如图,等边△AOB中点O是原点,点A在y轴上,点B的坐标是(2$\sqrt{3}$,2),小明做一个数学实验,在x轴上取一动点C,以AC为一边画出等边△ACP,移动点C时,探究点P的位置变化情况.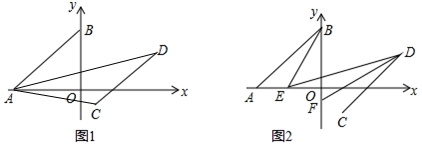
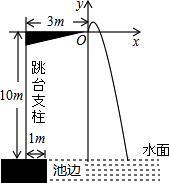 如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.
如图,2016年里约奥运会上,某运动员在10米跳台跳水比赛时估测身体(看成一点)在空中的运动路线是抛物线y=-$\frac{25}{6}$x2+$\frac{10}{3}$x(图中标出的数据为已知条件),运动员在空中运动的最大高度离水面为$10\frac{2}{3}$米.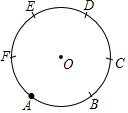 尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )
尺规作图特有的魅力曾使无数人沉湎其中,连当年叱咤风云的拿破仑也不例外,我们可以只用圆规将圆等分.例如可将圆6等分,如图只需在⊙O上任取点A,从点A开始,以⊙O的半径为半径,在⊙O上依次截取点B,C,D,E,F.从而点A,B,C,D,E,F把⊙O六等分.下列可以只用圆规等分的是( )