题目内容
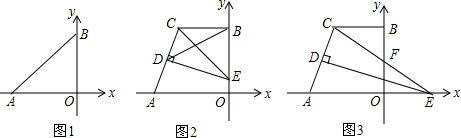
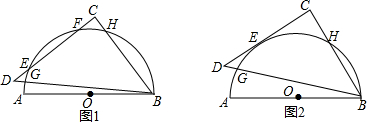
3.已知一个零刻度落在点A的量角器(半圆O)的直径为AB,等腰直角△BCD绕点B旋转.(1)如图1,当等腰直角△BCD运动至斜边BD交量角器边缘于点G,直角边CD交量角器边缘于点E,F,第三边交量角器边缘于点H时,点G在量角器上的读数为20°,求此时点H在量角器上的读数.
(2)如图2,当点G,E在量角器上的读数α,β满足什么关系时,等腰直角△BCD的直角边CD会与半圆O相切于点E?请说明理由.
分析 (1)连接OG、OH.由题意可知:∠AOG=20°,由等腰直角三角形的性质可求得∠CBD=45°,接下来,依据圆周角定理可求得∠HOG=90°,最后依据∠AOH=∠AOG+∠GOH求解即可;
(2)连接OG、OE.先由切线的性质证明OE⊥DC,然后依据平行线的判定定理可证明EO∥CB,接下来依据平行线的性质和可得到∠EOA=∠CBA,最后结合圆周角定理以及∠ABC、∠ABG、∠DBC的关系可得到α、β的关系.
解答 解:(1)如图1所示:连接OG、OH.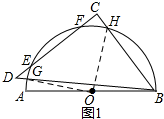
∵点G在量角器上的读数为20°,
∴∠AOG=20°.
∵△BCD为等腰直角三角形,
∴∠CBD=45°.
∴∠HOG=90°.
∴∠AOH=∠AOG+∠GOH=20°+90°=110°.
(2)如图2所示:连接OG、OE.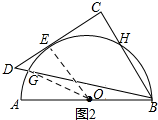
∵DC为圆O的切线,E为切点,
∴∠OED=90°.
∴∠OED=∠C.
∴EO∥CB.
∴∠EOA=∠CBA=β.
又∵∠GBA=$\frac{1}{2}$∠GOA=$\frac{1}{2}$α,∠ABC=∠ABG+∠DBC,
∴β=$\frac{1}{2}α$+45°.
点评 本题主要考查的是切线的性质和圆周角定理的应用,正确∠AOE=∠CBA=∠ABG+∠DBC是解题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
11.下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )
| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 6,7,8 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
5.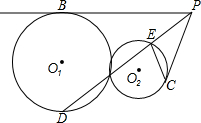 如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
 如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )
如图,⊙O1与⊙O2外切点A,半径为r1,r2,PB,PC分别为两圆的切线,B,C为切点,PB:PC=r1:r2,又PA交⊙O2于点E,则下面结论不正确的是( )| A. | S△PAB:S△PCE=r12:r22 | B. | PA:PD=r2:r1 | ||
| C. | AE:AD=r2:r1 | D. | PB:PD=r2:r1 |
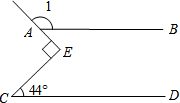 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.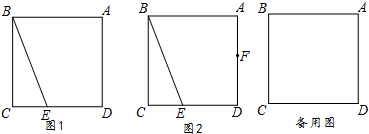
 如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)
如图,四边形ABCD是矩形,将矩形折叠,使得点D落在BC边上.折痕经过点A,作出折叠后的图形(要求尺规作图,保留作图痕迹,不写作法)