题目内容
2.定义:有一个内角为90°,且对角线相等的四边形称为准矩形.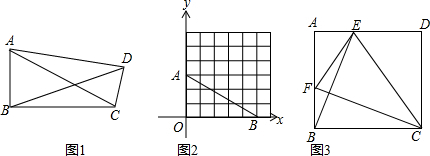
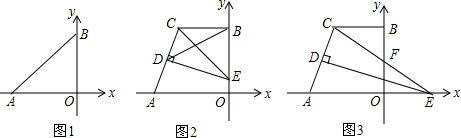
(1)①如图1,准矩形ABCD中,∠ABC=90°,若AB=2,BC=3,则BD=$\sqrt{13}$;
②如图2,直角坐标系中,A(0,3),B(5,0),若整点P使得四边形AOBP是准矩形,则点P的坐标是(5,3),(3,5);(整点指横坐标、纵坐标都为整数的点)
(2)如图3,正方形ABCD中,点E、F分别是边AD、AB上的点,且CF⊥BE,求证:四边形BCEF是准矩形;
(3)已知,准矩形ABCD中,∠ABC=90°,∠BAC=60°,AB=2,当△ADC为等腰三角形时,请直接写出这个准矩形的面积是$\sqrt{15}$+$\sqrt{3}$,$\sqrt{39}$+$\sqrt{3}$,2$\sqrt{15}$.
分析 (1)利用准矩形的定义和勾股定理计算,再根据准矩形的特点和整点的特点求出即可;
(2)先利用正方形的性质判断出△ABE≌△BCF,即可;
(2)分三种情况分别计算,用到梯形面积公式,对角线面积公式,对角线互相垂直的四边形的面积计算方法.
解答 解:(1)①∵∠ABC=90,
∴BD=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{4+9}$=$\sqrt{13}$,
故答案为$\sqrt{13}$,
②∵A(0,3),B(5,0),
∴AB=$\sqrt{{5}^{2}+{3}^{2}}$=6,
设点P(m,n),A(0,0),
∴OP=$\sqrt{{m}^{2}+{n}^{2}}$=6,
∵m,n都为整数,
∴点P(3,5)或(5,3);
故答案为P(3,5)或(5,3);
(2)∵四边形ABCD是正方形,
∴AB=BC∠A=∠ABC=90°,
∴∠EAF+∠EBC=90°,
∵BE⊥CF,
∴∠EBC+∠BCF=90°,
∴∠EBF=∠BCF,
∴△ABE≌△BCF,
∴BE=CF,
∴四边形BCEF是准矩形;
(3)$\sqrt{15}+\sqrt{3}$,$\sqrt{39}+\sqrt{3}$,$2\sqrt{15}$
∵∠ABC=90°,∠BAC=60°,AB=2,
∴BC=2$\sqrt{3}$,AC=4,
准矩形ABCD中,BD=AC=4,
①当AC=AD时,如图1,作DE⊥AB,
∴AE=BE$\frac{1}{2}$AB=1,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=$\sqrt{16-1}$=$\sqrt{15}$,
∴S准矩形ABCD=S△ADE+S梯形BCDE
=$\frac{1}{2}$DE×AE+$\frac{1}{2}$(BC+DE)×BE
=$\frac{1}{2}$×$\sqrt{15}$+$\frac{1}{2}$(2$\sqrt{3}$+$\sqrt{15}$)×1
=$\sqrt{15}$+$\sqrt{3}$;
②当AC=CD时,如图2,
作DF⊥BC,
∴BD=CD,
∴BF=CF=$\frac{1}{2}$BC=$\sqrt{3}$,
∴DF=$\sqrt{C{D}^{2}-C{F}^{2}}$=$\sqrt{16-3}$=$\sqrt{13}$,
∴S准矩形ABCD=S△DCF+S梯形ABFD
=$\frac{1}{2}$FC×DF+$\frac{1}{2}$(AB+DF)×BF
=$\frac{1}{2}$×$\sqrt{3}$×$\sqrt{13}$+$\frac{1}{2}$(2+$\sqrt{13}$)×$\sqrt{3}$
=$\sqrt{39}$+$\sqrt{3}$;
③当AD=CD,如图3,
连接AC中点和D并延长交BC于M,连接AM,连接BG,过B作BH⊥DG,
在Rt△ABC中,AC=2AB=4,
∴BD=AC=4,
∴AG=$\frac{1}{2}$AC=2,
∵AB=2,
∴AB=AG,
∵∠BAC=60°,
∴∠ABG=60°,
∴∠CBG=30°
在Rt△BHG中,BG=2,∠BGH=30°,
∴BH=1,
在Rt△BHM中,BH=1,∠CBH=30°,
∴BM=$\frac{2\sqrt{3}}{3}$,HM=$\frac{\sqrt{3}}{3}$,
∴CM=$\frac{4\sqrt{3}}{3}$,
在Rt△DHB中,BH=1,BD=4,
∴DH=$\sqrt{15}$,∴DM=DH-MH=$\sqrt{15}$-$\frac{\sqrt{3}}{3}$,
∴S准矩形ABCD=S△ABM+S四边形AMCD,
=$\frac{1}{2}$BM×AB+$\frac{1}{2}$AC×DM
=$\frac{1}{2}$×$\frac{2\sqrt{3}}{3}$×2+$\frac{1}{2}$×4×($\sqrt{15}$-$\frac{\sqrt{3}}{3}$)
=2$\sqrt{15}$;
故答案为$\sqrt{15}$+$\sqrt{3}$,$\sqrt{39}$+$\sqrt{3}$,2$\sqrt{15}$.
点评 此题是四边形综合题,主要考查了新定义,勾股定理,梯形面积公式,对角线面积公式,三角形面积公式,分情况计算是解本题的难点.

 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案| A. | $\sqrt{3}$,$\sqrt{4}$,$\sqrt{5}$ | B. | 2,3,4 | C. | 6,7,8 | D. | 1,$\sqrt{2}$,$\sqrt{3}$ |
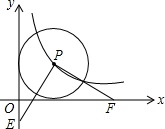 如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.
如图,点P为反比例函数y=$\frac{1}{x}$(x>0)图象上一点,以点P为圆心作圆,且该圆恰与两坐标轴都相切.在y轴任取一点E,连接PE并过点P作直线PE的垂线与x轴交于点F,则线段OE与线段OF的长度可能满足的数量关系式是OF-OE=2或OE-OF=2或OF+OE=2.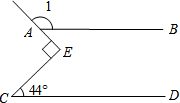 如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.
如图,直线AB∥CD,∠C=44°,∠E为直角,则∠1=134°.