题目内容
7.在平面直角坐标系xOy中,一次函数y=$\frac{1}{2}$x+b的图象与y轴交于点A,与反比例函数y=$\frac{8}{x}$的图象交于点P(2,m).(1)求m与b的值;
(2)取OP的中点B,若△MPO与△AOP关于点B中心对称,求点M的坐标.
分析 (1)把P(2,m)分别代入y=$\frac{1}{2}$x+b与y=$\frac{8}{x}$中即可得到结论;
(2)由于一次函数y=$\frac{1}{2}$x+b的图象与y轴交于点A,求得A(0,3),由B为OP的中点,于是得到B(1,2),于是得到结论.
解答  解:(1)∵y=$\frac{1}{2}$x+b的图象与y=$\frac{8}{x}$的图象交于点P(2,m),
解:(1)∵y=$\frac{1}{2}$x+b的图象与y=$\frac{8}{x}$的图象交于点P(2,m),
∴m=4,b=3;
(2)∵一次函数y=$\frac{1}{2}$x+b的图象与y轴交于点A,
∴A(0,3),
∵B为OP的中点,
∴B(1,2),
∴点A关于点B对称点M的坐标为(2,1).
点评 本题考查了反比例函数与一次函数的交点,中心对称的性质,正确的进行计算是解题的关键.

练习册系列答案
相关题目
18.下列实数中,为无理数的是( )
| A. | $\sqrt{2}$ | B. | $\frac{1}{2}$ | C. | 0.2 | D. | -7 |
2.在下列实数中,无理数是( )
| A. | sin45° | B. | $\frac{1}{3}$ | C. | 0.$\stackrel{•}{3}$ | D. | 3014 |
12.已知方程x2+kx-6=0的一个根是x=2,则它的另一个根为( )
| A. | x=1 | B. | x=-2 | C. | x=3 | D. | x=-3 |
19.在实数$-\sqrt{3}$,-2,0,3中,大小在-1和2之间的数是( )
| A. | $-\sqrt{3}$ | B. | -2 | C. | 0 | D. | 3 |
16.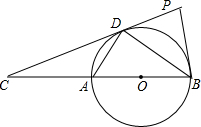 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
 如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )
如图所示,直线CD与以线段AB为直径的圆相切于点D并交BA的延长线于点C,且AB=2,AD=1,P点在切线CD的延长线上移动时,则△PBD的外接圆的半径的最小值为( )| A. | 1 | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{2}$ |
17. 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
 如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )
如图,△ABC内接于⊙O,连接OA,OB,∠C=40°,则∠OBA的度数是( )| A. | 60° | B. | 50° | C. | 45° | D. | 40° |
 如图,△ABC中,AB=AC,将△ABC绕点A逆时针旋转60°后得到△ADE,若AB=1,则CE的长为1.
如图,△ABC中,AB=AC,将△ABC绕点A逆时针旋转60°后得到△ADE,若AB=1,则CE的长为1.