题目内容
16.某初中2013年、2014年分别选拔了7名学生参加区级“综合体能”竞赛,学校想了解2014年选拔的7名学生的实力,于是在3月1日进行了一次与2013年项目、评分方法完全一样的测试.两年成绩如下表所示:| 2013年 | 58 | 65 | 70 | 70 | 70 | 75 | 82 |
| 2014年 | 50 | 55 | 70 | 75 | 78 | 80 | 82 |
(3)经计算,2014年选拔的7名学生成绩的方差为136.9,那么哪年选拔的7名学生成绩较为整齐?通过计算说明;
(3)除上述问题(1)(2)外,根据题中情境提出一个问题,不必解答.
分析 (1)根据中位数和平均数的定义即可求解;
(2)先根据方差的定义求出2013年的7名学生成绩的方差,再与2014年进行比较,方差较小的成绩较为整齐;
(3)直接利用中位数或平均数的意义提出问题即可.
解答 解:(1)2013年7个数据中,第四个是70,所以中位数是70,
2014年年7个数据中,第四个是75,所以中位数是75;
2013年7个数据的平均数为:$\frac{1}{7}$(58+65+70+70+70+75+82)=$\frac{1}{7}$×490=70,
2014年7个数据的平均数为:$\frac{1}{7}$(50+55+70+75+78+80+82)=$\frac{1}{7}$×490=70;
(3)2013年的7名学生的成绩较为整齐.理由如下:
∵${s}_{2013}^{2}$=$\frac{1}{7}$[(58-70)2+(65-70)2+3×(70-70)2+(75-70)2+(82-70)2]≈48.29,
S20142≈136.86,
∴${s}_{2013}^{2}$<S20142,
∴2013年的7名学生的成绩较为整齐;
(3)可以为:利用(1)中所求,比较两年竞赛成绩.
点评 本题考查的是方差、中位数、平均数的求法和意义,读懂统计图,从统计图中得到必要的信息是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6. 如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
 如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )
如图,在△ABC中,D、E分别是AC、AB上的点,在△ADE≌△BDE≌△BDC,则∠A的度数是( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
4.已知样本数据2,3,5,4,6,下列说法不正确的是( )
| A. | 平均数是4 | B. | 中位数是5 | C. | 标准差是$\sqrt{2}$ | D. | 方差是2 |
6.某销售公司有营销人员15人,销售部为了制定某种商品的月销售量定额,统计了这15人某月的销售量,如表所示:
那么这15位销售人员该月销售量的众数、中位数分别是210件、210件.
| 每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
| 人数 | 1 | 1 | 3 | 5 | 3 | 2 |
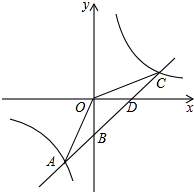 如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D.
如图,一次函数y1=kx+b的图象与反比例函数y2=$\frac{m}{x}$的图象交于点A(-2,-5),C(5,n),交y轴于点B,交x轴于点D. 如图,三角形ABC以O为旋转中心,顺时针方向旋转60°,请作出旋转后的图形.
如图,三角形ABC以O为旋转中心,顺时针方向旋转60°,请作出旋转后的图形.