题目内容
 如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=
如图,在△ABC中,BA=BC,D,E是AC边上的两点,且满足∠DBE=| 1 |
| 2 |
| 1 |
| 2 |
考点:旋转的性质
专题:证明题
分析:根据旋转的定义可知∠ABC=∠E′BE=2∠DBE,可得到∠E′BD=∠EBD,证明△BE′D≌△BED即可得到DE′=DE.
解答:证明:
∵△BEC按逆时针旋转,得到△BE′A,且AB=BC,
∴BE′=BE,∠E′BE=∠ABC,
∵∠DBE=
∠ABC,
∴∠E′BE=2∠DBE,
∴∠E′BD=∠EBD,
在△BE′D和△BED中
∴△BE′D≌△BED(SAS),
∴DE′=DE.
∵△BEC按逆时针旋转,得到△BE′A,且AB=BC,
∴BE′=BE,∠E′BE=∠ABC,
∵∠DBE=
| 1 |
| 2 |
∴∠E′BE=2∠DBE,
∴∠E′BD=∠EBD,
在△BE′D和△BED中
|
∴△BE′D≌△BED(SAS),
∴DE′=DE.
点评:本题主要考查旋转的性质和全等三角形的判定,掌握旋转角相等是解题的关键.本题也可以利用对应角相等得出∠E′BD=∠EBD.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
 如图是用两种正多边形密铺的平面图形图案中的一部分,其中一种是正方形,另一种与正方形相邻的四个正多边形是全等图形,那么这种正多边形是( )
如图是用两种正多边形密铺的平面图形图案中的一部分,其中一种是正方形,另一种与正方形相邻的四个正多边形是全等图形,那么这种正多边形是( )| A、正五边形、轴对称图形 |
| B、正六边形、中心对称图形 |
| C、正七边形、轴对称图形 |
| D、正八边形、中心对称图形 |
计算(-2)2011×(0.5)2010等于( )
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
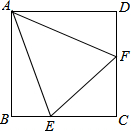 如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是
如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是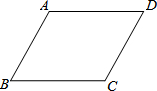 已知:如图,AB=DC,AD=BC.(提示:连接BD)
已知:如图,AB=DC,AD=BC.(提示:连接BD)