题目内容
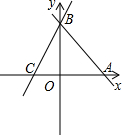 直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.
直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,过点B的直线交x轴负半轴于C,且OB:OC=3:1.(1)求点B的坐标;
(2)求直线BC的解析式.
考点:两条直线相交或平行问题
专题:
分析:(1)首先将B点坐标代入y=-x-b求出b的值,进而求出B点坐标;
(2)利用OB:OC=3:1,得出C点坐标,再利用待定系数法求一次函数解析式.
(2)利用OB:OC=3:1,得出C点坐标,再利用待定系数法求一次函数解析式.
解答:解:(1)∵直线AB:y=-x-b分别与x,y轴交于A(6,0)、B两点,
∴0=-6-b,
解得:b=-6,
则y=-x+6,
当x=0,则y=6,
故B点坐标为:(0,6);
(2)∵OB:OC=3:1,
∴CO=2,
则C点坐标为:(-2,0),
将B,C点代入直线BC的解析式y=kx+a中,
则
,
解得:
,
故直线BC的解析式为:y=3x+6.
∴0=-6-b,
解得:b=-6,
则y=-x+6,
当x=0,则y=6,
故B点坐标为:(0,6);
(2)∵OB:OC=3:1,
∴CO=2,
则C点坐标为:(-2,0),
将B,C点代入直线BC的解析式y=kx+a中,
则
|
解得:
|
故直线BC的解析式为:y=3x+6.
点评:此题主要考查了坐标与图形的性质以及待定系数法求一次函数解析式,得出B点坐标是解题关键.

练习册系列答案
相关题目
 如图,每个小正方形的边长都等于1,则△ABC的外心坐标是
如图,每个小正方形的边长都等于1,则△ABC的外心坐标是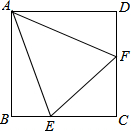 如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是
如图,在正方形ABCD中,∠EAF=45°,BE=2,DF=6,则EF的长是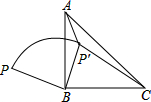 如图,P是等腰Rt△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1:
如图,P是等腰Rt△ABC外一点,把BP绕点B顺时针旋转90°到BP′,已知∠AP′B=135°,P′A:P′C=1: