题目内容
11.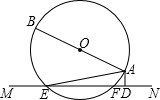 如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.
如图:AB是⊙O的直径,直线MN与⊙O相交于点E、F,AD⊥MN,垂足为D.(1)求证:∠BAE=∠DAF;
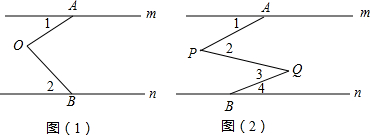
(2)若把直线MN向上平行移动,使它与AB相交,其它条件不变,请把变化后的图形画出来,并把出∠BAE与∠DAF是否仍然相等(直接回答,不必证明)
分析 (1)连接BE,根据AB是⊙O的直径,AD⊥MN,得到∠BEA=90°,∠ADF=90°,由四边形ABEF是圆内接四边形,得到∠AFD=∠B,等量代换得到∠BAE=∠DAF;
(2)如图2,连接BE,根据AB是⊙O的直径,AD⊥MN,得到∠BEA=90°,∠ADF=90°,根据同弧所对的圆周角相等得到∠AFD=∠B,等量代换得到∠BAE=∠DAF.
解答  证明:(1)如图1,连接BE,
证明:(1)如图1,连接BE,
∵AB是⊙O的直径,
∴∠BEA=90°,
∴∠B+∠BAE=90°,
∵AD⊥MN,
∴∠ADF=90°,
∴∠FAD+∠AFD=90°,
∵四边形ABEF是圆内接四边形,
∴∠AFD=∠B,
∴∠BAE=∠DAF;
(2)如图2,相等; 证明:连接BE,
证明:连接BE,
∵AB是⊙O的直径,
∴∠BEA=90°,
∴∠B+∠BAE=90°,
∵AD⊥MN,
∴∠ADF=90°,
∴∠FAD+∠AFD=90°,
∵∠AFD=∠B,
∴∠BAE=∠DAF.
点评 本题考查了圆周角定理及其推论,圆内接四边形的性质.注意解决一题多变的方法,思路一般大体相同.

练习册系列答案
相关题目
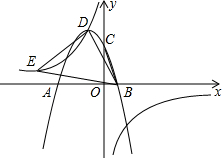 如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.
如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.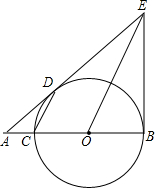 已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根
已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根