题目内容
4.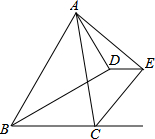 在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.
在△ABC中,BD平分∠ABC,CE平分∠ACB的外角,AD⊥BD,AE⊥CE,若DE=$\frac{3}{2}$,AE=$\frac{7}{2}$,∠ABC=60°,则AB=5.
分析 延长AE交BC于点N,作NH⊥AD于点H,利用全等三角形证明D、E分别是AM和AN的中点,则MN即可求得,在直角△MNH中利用三角函数求得HM和HN的长,再在直角△AHN中利用勾股定理求得AH的长,则AB=AM=AH-MH求解.
解答  解:延长AE交BC于点N,作NH⊥AD于点H.
解:延长AE交BC于点N,作NH⊥AD于点H.
在直角△ABD和直角△MBD中,
$\left\{\begin{array}{l}{∠ABD=∠MBD}\\{BD=BD}\\{∠ADB=∠BDM=90°}\end{array}\right.$,
∴△ABD≌△MBD(ASA),
∴AD=DM,AB=BM,
同理,AE=EN,AN=2AE=7,
∴DE是△AMN的中位线,
∴MN=2DE=2×$\frac{3}{2}$=3,
又∵∠ABM=60°,AB=BM,
∴△ABC是等边三角形,
∴∠AMB=60°,
∴∠NMH=∠AMB=60°,
∴在直角△MNH中,NH=MN•sin60°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,MH=MN•cos60°=3×$\frac{1}{2}$=$\frac{3}{2}$.
在直角△ANH中,AH=$\sqrt{A{N}^{2}-H{N}^{2}}$=$\sqrt{{7}^{2}-(\frac{3\sqrt{3}}{2})^{2}}$=$\frac{13}{2}$,
∴AM=AH-MH=$\frac{13}{2}-\frac{3}{2}$=5.
∴AB=AM=5.
故答案是:5.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,等腰三角形的判定与性质,熟记性质与定理并作辅助线构造出以DE为中位线的三角形是解题的关键.

练习册系列答案
相关题目
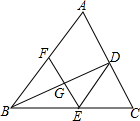 如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.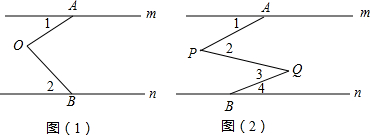
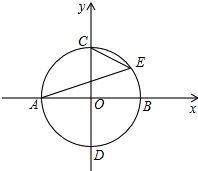 如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..
如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..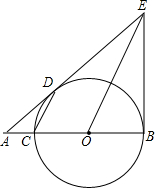 已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根
已知如图,BC是圆O直径,BE是圆O的切线,切点为B,OE平行于弦CD,ED,BC的延长线交于点A,若AC=1,且AC,AD的长是关于x的方程x2-mx+2=0的两个根
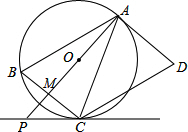 如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.
如图,AD是⊙O的切线,切点为A,AB是⊙O的弦,过点B作BC∥AD,交⊙O于点C,连接AC,过点C作CD∥AB,交AD于点D,连接AO并延长交BC于点M,交过点C的直线于点P,且∠BCP=∠ACD.