题目内容
19. 如图,在梯形ABCD中,AD∥BC,E是AB的中点,EF⊥CD于点F,求证:S梯形ABCD=EF•CD.
如图,在梯形ABCD中,AD∥BC,E是AB的中点,EF⊥CD于点F,求证:S梯形ABCD=EF•CD.
分析 作延长DE交CD延长线上点G,过点G作GH⊥FE,交FE的延长线上于点H,然后将梯形ABCD的面积转化为梯形HGFC的面积,即可求解.
解答  解:延长DE交CB延长线上点G,过点G作GH⊥FE,交FE的延长线上于点H,
解:延长DE交CB延长线上点G,过点G作GH⊥FE,交FE的延长线上于点H,
∵AD∥BC,E是AB中点,
∴∠A=∠EBG,AE=BE,
在△AED和△BGE中,
$\left\{\begin{array}{l}{∠A=∠EBG}&{\;}\\{AE=BE}&{\;}\\{∠AED=∠BEG}&{\;}\end{array}\right.$,
∴△AED≌△BGE(ASA),
∴GE=ED,即点E是GD的中点,
∵∠H=∠DFH=90°,
∴CD∥HG,
同理:△GHE≌△DFE,
∴GH=DF,HE=EF,
∴GH+CF=CF+DF=CD,
∴梯形ABCD与梯形HGFC的面积相等,
∵S梯形HGFC=$\frac{1}{2}$(GH+CF)•HF=$\frac{1}{2}$×CD×2EF=EF•CD.
点评 本题考查了梯形的性质、全等三角形的判定与性质;本题通过作辅助线,把梯形ABCD的面积转化为梯形HGFC的面积是解决问题的关键.

练习册系列答案
相关题目
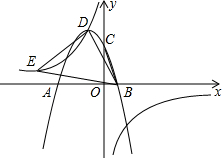 如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.
如图,抛物线y=ax2+2ax+c(a≠0)交x轴于点A(-3,0)与点B,与y轴交于点C,tan∠ABC=3,双曲线$y=\frac{k}{x}(k≠0)$经过抛物线的顶点D.