题目内容
4．已知$\frac{x}{y}=\frac{4}{3}$，那么$\frac{3x-2y}{2x+3y}$=$\frac{6}{17}$．分析 根据比例的性质，可用y表示x，根据分式的性质，可得答案．
解答 解：由$\frac{x}{y}=\frac{4}{3}$，得
x=$\frac{4}{3}$y．
$\frac{3x-2y}{2x+3y}$=$\frac{3×\frac{4y}{3}-2y}{2×\frac{4y}{3}+3y}$=$\frac{6}{17}$，
故答案为：$\frac{6}{17}$．
点评 本题考查了比例的性质，利用比例的性质得出x=$\frac{4}{3}$y是解题关键．
练习册系列答案
品学双优卷系列答案
小学期末冲刺100分系列答案
相关题目
14．
如图，△ABC的三个顶点都在正方形网格的格点上，则sin∠A的值为（ ）
如图，△ABC的三个顶点都在正方形网格的格点上，则sin∠A的值为（ ）| A． | $\frac{6}{5}$ | B． | $\frac{5}{6}$ | C． | $\frac{\sqrt{34}}{3}$ | D． | $\frac{5\sqrt{61}}{61}$ |
如图，△ABC内接于⊙O，∠ABC=120°，AB=BC，AD为⊙O的直径，AD=8，求BD的长．
为加强我县创建文明卫生县城宣传力度，需要在甲楼A处到E处悬挂一幅宣传条幅，在乙楼顶部D点测得条幅顶端A点的仰角为45°，条幅底端E点的仰角为30°，若甲、乙两楼的水平距离BC为21米，求条幅的长约是多少米？（结果精确到0.1米）．
16．已知x2+3xy+y2=0（x≠0，y≠0），则分式$\frac{y}{x}+\frac{x}{y}$的值等于（ ）
| A． | $\frac{1}{3}$ | B． | -$\frac{1}{3}$ | C． | 3 | D． | -3 |
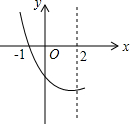如图，是抛物线y=ax2+bx+c（a≠0）的一部分，已知抛物线的对称轴为x=2，与x轴的一个交点是（-1，0），则方程ax2+bx+c=0（a≠0）的两根是x1=-1，x2=5．