题目内容
14.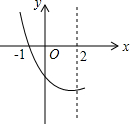 如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),则方程ax2+bx+c=0(a≠0)的两根是x1=-1,x2=5.
如图,是抛物线y=ax2+bx+c(a≠0)的一部分,已知抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),则方程ax2+bx+c=0(a≠0)的两根是x1=-1,x2=5.
分析 根据二次函数的对称性求出抛物线与x轴的另一交点,然后根据二次函数与一元二次方程的关系写出即可.
解答 解:∵抛物线的对称轴为x=2,与x轴的一个交点是(-1,0),
∴抛物线与x轴的另一交点是(5,0),
∴方程ax2+bx+c=0(a≠0)的两根是x1=-1,x2=5.
故答案为:x1=-1,x2=5.
点评 本题考查了抛物线与x轴的交点,一元二次方程与二次函数的关系,难点在于熟练掌握二次函数的对称性确定出与x轴的另一交点坐标.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案
相关题目
5.下列图形不是轴对称图形的是( )
| A. | 直线 | B. | 线段 | C. | 平行四边形 | D. | 角 |
2.点A(4,a)与点B(b,3)关于x轴对称,那么a的值为( )
| A. | 3 | B. | -3 | C. | 4 | D. | -4 |
9.下列事件中是必然事件的是( )
| A. | 三角形内心到三个顶点的距离相等 | B. | 方程x2-2x+1=0有两个不等实根 | ||
| C. | y=ax2+bx+c是二次函数 | D. | 圆的切线垂直于经过切点的半径 |
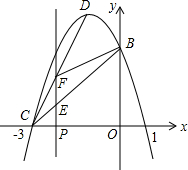 如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).
如图,抛物线y=ax2+bx+c与x轴的交点为点A(1,0)和点C(-3,0),与y轴的交点为点B(0,3).