题目内容
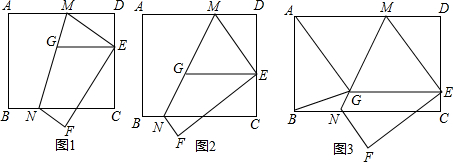
5.在矩形ABCD中,点M、N分别在AD、BC上,将矩形沿着MN折叠(点A的对称点为E,点B的对称点为F),点E在CD上,过点E作EG∥AD,交MN于点G.(1)如图1,求证:△EMG是等腰三角形;
(2)如图2,若AD=2DE,求∠MEG的正切值;
(3)在(2)的条件下,如图3,连接AG、BG,若△ABG的面积为$\frac{15}{12}$,AB=AM,求NG的长.
分析 (1)运用平行线的性质和折叠的性质即可证明;
(2)设DE=x,DM=r,根据题意用x表示r即可求解;
(3)过点M作MK⊥EG,过点G作GL⊥NC,延长EG交AB于点H,用含有x的代数式表示△ABG的面积,进而求出x的值,证明△MGK∽△GNL即可求解.
解答 解:(1)如图1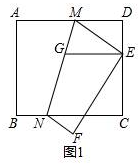
∵EG∥AD,
∴∠AMN=∠MGE,
∵∠AMN=∠EMG,
∴∠MGE=∠EMG,
∴△EMG是等腰三角形;
(2)如图2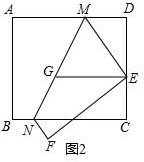
设DE=x,DM=r,则有AD=2x,ME=AM=2x-r,
在直角三角形MDE中,MD2+DE2=ME2,
r2+x2=(2x-r)2,
解得:r=$\frac{3}{4}x$,
∴DM=$\frac{3}{4}x$,ME=$\frac{5}{4}x$,
∵EG∥AD,
∴tan∠MEG=tan∠DME=$\frac{DE}{DM}$=$\frac{4}{3}$,
(3)如图3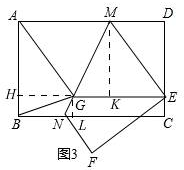
由(1)知,EM=EG,
又∵AM=EM,
∴AM=EG,
∵AM∥EG,
所以可证四边形AMEG是菱形,
由(2)知,AM=EM=EG=$\frac{5}{4}x$,
∴AB=AM=$\frac{5}{4}x$,
过点M作MK⊥EG,过点G作GL⊥NC,延长EG交AB于点H,
易证四边形MKED和四边形CEGL是矩形,GH⊥AB,
∴MK=DE=x,GL=AB-MK=$\frac{1}{4}x$
∴GK=$\frac{1}{2}x$,GH=2x-$\frac{5}{4}x$=$\frac{3}{4}x$,
由△ABG的面积为$\frac{15}{12}$可得:$\frac{1}{2}$×$\frac{5}{4}x$×$\frac{3}{4}x$=$\frac{15}{12}$,
解得:x=$\frac{2\sqrt{6}}{3}$,
在直角三角形MKG中,MG=$\sqrt{M{K}^{2}+G{K}^{2}}$=$\frac{\sqrt{5}}{2}$x,
∵GE∥CN,
∴∠MGK=∠GNL,
∵∠GLN=∠MKG=90°,
∴△MGK∽△GNL,
∴$\frac{MG}{GN}=\frac{MK}{GL}=\frac{4}{1}$,
∴GN=$\frac{1}{4}$×$\frac{\sqrt{5}}{2}$x=$\frac{\sqrt{5}}{8}×$$\frac{2\sqrt{6}}{3}$=$\frac{\sqrt{30}}{12}$.
点评 此题主要考查几何变换中的翻折,会熟练运用翻折的性质确定相等的线段和角,会运用勾股定理建立等量关系求解线段,会运用相似建立关系求线段长度是解题的关键.

 学习实践园地系列答案
学习实践园地系列答案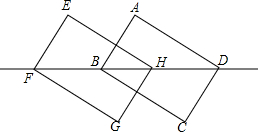 如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )
如图,在长方形ABCD中,AB=CD=6,AD=BC=8,对角线BD=10,现将长方形沿对角线BD所在直线向左平移4个单位得到长方形EFGH,则点F到直线AD的距离是( )| A. | 8 | B. | 8.4 | C. | 9 | D. | 10 |
| A. | 1道 | B. | 2道 | C. | 3道 | D. | 4道 |
| A. | sinα的值越大,梯子越陡 | B. | cosα的值越大,梯子越陡 | ||
| C. | tanα的值越小,梯子越陡 | D. | 陡缓程度与α的函数值无关 |
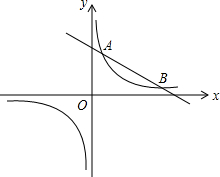 如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.
如图,双曲线y=$\frac{k}{x}$(k>0)与直线y=-$\frac{1}{2}$x+4相交于A,B两点.