题目内容
13.一根台式弹簧秤的原长为12cm,它能称的质量不超过20kg,并且每增加1kg就缩短$\frac{1}{2}$cm.(1)写出放物体后的弹簧长度y(cm)与所放物体质量x(kg)之间的函数表达式;
(2)求自变量x的取值范围;
(3)当放重物10kg后,求此弹簧的长度;
(4)弹簧长度为4cm时,求此时所放物体的质量.弹簧的长度能否为1cm?
分析 (1)根据弹簧长度与物体重量间的数量关系,列出y关于x的函数表达式;
(2)由该弹簧秤能称的质量不超过20kg,可得出x的取值范围;
(3)将x=10代入函数表达式中,求出y值即可;
(4)令y=4,得出关于x的一元一次方程,解方程即可得出结论;代入x的最大值,得出y最小值为2,由此可得出弹簧的长度不能为1cm.
解答 解:(1)根据已知可得:y=-$\frac{1}{2}$x+12.
(2)由题意可知:0≤x≤20.
(3)令x=10,则y=-$\frac{1}{2}$×10+12=7.
答:当放重物10kg后,此弹簧的长度为7cm.
(4)令y=4,则-$\frac{1}{2}$x+12=4,
解得:x=16.
故弹簧长度为4cm时,此时所放物体的质量为16kg.
令x=20,则y=-$\frac{1}{2}$×20+12=2.
1<2,故弹簧的长度不能为1cm.
点评 本题考查了一次函数的应用,解题的关键:(1)根据数量关系得出函数表达式;(2)根据已知寻找x的取值范围;(3)将x=10代入函数表达式;(4)将y=4代入函数表达式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系寻找出函数关系式,在由函数的单调性去寻找最值即可.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
1.若y=$\sqrt{x-\frac{1}{2}}$+$\sqrt{\frac{1}{2}-x}$-3,则xy的值为( )
| A. | -8 | B. | -$\frac{1}{8}$ | C. | 8 | D. | $\frac{1}{8}$ |
2.下列有关对顶角的说法中,正确的是( )
| A. | 相交的两条直线只能组成1对对顶角 | |
| B. | 相等的角是对顶角 | |
| C. | 若两个角不是对顶角,则这两个角不相等 | |
| D. | 若两个角不相等,则这两个角一定不是对顶角 |
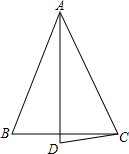 如图,在△ABC中,∠B=∠C,点D在△ABC外,∠ADC=∠ACD.
如图,在△ABC中,∠B=∠C,点D在△ABC外,∠ADC=∠ACD.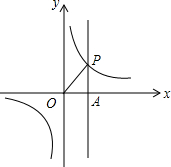 如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.
如图,函数y=$\frac{k}{x}$的图象与直线x=2交于第一象限的点P,△AOP的面积等于$\frac{1}{2}$.