题目内容
14.计算:$\frac{{2{x^3}}}{y}÷\frac{4x}{{3{y^2}}}$=$\frac{3{x}^{2}y}{2}$;
$\frac{4a}{{{a^2}-1}}+\frac{1+a}{1-a}$=-$\frac{a-1}{a+1}$.
分析 原式利用除法法则变形,约分即可得到结果;原式通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:原式=$\frac{2{x}^{3}}{y}$•$\frac{3{y}^{2}}{4x}$=$\frac{{3{x^2}y}}{2}$;
原式=$\frac{4a}{(a+1)(a-1)}$-$\frac{(a+1)^{2}}{(a+1)(a-1)}$=-$\frac{a-1}{a+1}$,
故答案为:$\frac{3{x}^{2}y}{2}$;-$\frac{a-1}{a+1}$
点评 此题考查了分式的乘除法,以及分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.下列有关对顶角的说法中,正确的是( )
| A. | 相交的两条直线只能组成1对对顶角 | |
| B. | 相等的角是对顶角 | |
| C. | 若两个角不是对顶角,则这两个角不相等 | |
| D. | 若两个角不相等,则这两个角一定不是对顶角 |
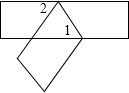 如图,折叠宽度相等的长方形纸条,若∠1=62°,则∠2=56度.
如图,折叠宽度相等的长方形纸条,若∠1=62°,则∠2=56度.
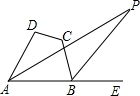 如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.
如图,在四边形ABCD中,∠DAB的角平分线与∠ABC的外角平分线相交于点P,且∠D+∠C=240°,则∠P=30°.