题目内容
5.解方程组:$\left\{\begin{array}{l}x+2y=1\\{x^2}-3xy+2{y^2}=0\end{array}\right.$.分析 先将第2个方程变形为x-2y=0,x-y=0,从而得到两个二元一次方程组,再分别求解即可.
解答 解:$\left\{\begin{array}{l}{x+2y=1①}\\{{x}^{2}-3xy+2{y}^{2}=0②}\end{array}\right.$
由②得:x-2y=0,x-y=0,
原方程组可化为$\left\{\begin{array}{l}x+2y=1\\ x-2y=0\end{array}\right.$,$\left\{\begin{array}{l}x+2y=1\\ x-y=0\end{array}\right.$,
故原方程组的解为$\left\{\begin{array}{l}x=\frac{1}{2}\\ y=\frac{1}{4}\end{array}\right.$,$\left\{\begin{array}{l}x=\frac{1}{3}\\ y=\frac{1}{3}\end{array}\right.$.
点评 本题考查的是高次方程,关键是通过分解,把高次方程降次,得到二元一次方程组,用到的知识点是因式分解、加减法.

练习册系列答案
相关题目
16.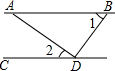 如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
 如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )
如图,AB∥CD,AD⊥BD,∠1=55°,则∠2的大小是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
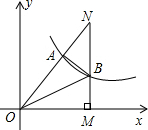 如图,双曲线y=$\frac{k}{x}$(k≠0)经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为10,则k的值是24.
如图,双曲线y=$\frac{k}{x}$(k≠0)经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为10,则k的值是24.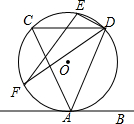 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$. 如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.
如图,小明在大楼30米高即(PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚处的俯角为60°.已知该山坡的坡度i(即tan∠ABC)为1:$\sqrt{3}$,点P,H,B,C,A在同一个平面上,点H、B、C在同一条直线上,且PH丄HC,则A到BC的距离为10$\sqrt{3}$米.