题目内容
10.有一块直角三角形的绿地,量得两直角边BC、AC分别为6m,8m,现在要将绿地扩充成等腰三角形,且扩充部分是以AC边为直角边的直角三角形,求扩充后等腰三角形绿地的面积.(图2,图3备用)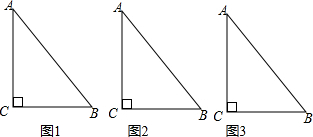
分析 根据勾股定理求出斜边AB,(1)当AB=AD时,求出CD即可;(2)当AB=BD时,求出CD、AD即可;(3)当DA=DB时,设AD=x,则CD=x-6,求出即可.
解答 解:
在Rt△ABC中,∵∠ACB=90°,AC=8m,BC=6m,
∴AB=10m,
(1)如图1,当AB=AD时,CD=6m,
则△ABD的面积为:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×(6+6)×8=48(m2);
(2)如图2,当AB=BD时,CD=4m,则△ABD的面积为:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×(6+4)×8=40(m2);
(3)如图3,当DA=DB时,设AD=x,则CD=x-6,
则x2=(x-6)2+82,
∴x=$\frac{25}{3}$,
则△ABD的面积为:$\frac{1}{2}$BD•AC=$\frac{1}{2}$×$\frac{25}{3}$×8=$\frac{100}{3}$(m2);
答:扩充后等腰三角形绿地的面积是48m2或40m2或$\frac{100}{3}$m2.
点评 本题主要考查对勾股定理,等腰三角形的性质等知识点的理解和掌握,能通过分类求出等腰三角形的所有情况是解此题的关键.

练习册系列答案
相关题目
6.下列四个命题,其中真命题有( )
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
15.化简$\sqrt{\frac{1}{8}}$,其结果是( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{8}}}{8}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | ±$\frac{{\sqrt{2}}}{4}$ |
2.在△ABC中,AB=BC=AC=6,则△ABC的面积为( )
| A. | 9 | B. | 18 | C. | 9$\sqrt{3}$ | D. | 18$\sqrt{3}$ |
 如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);
如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);
 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,求BC的长.
如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD=$\sqrt{5}$,求BC的长.