题目内容
13.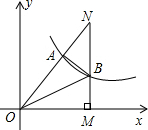 如图,双曲线y=$\frac{k}{x}$(k≠0)经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为10,则k的值是24.
如图,双曲线y=$\frac{k}{x}$(k≠0)经过Rt△OMN斜边上的点A,与直角边MN相交于点B,已知OA=2AN,△OAB的面积为10,则k的值是24.
分析 过点A作AC⊥x轴于点C,则AC∥MN,故可得出△OAC∽△OMN,由相似三角形的性质可知OC:OM=AC:MN=OA:ON,再由OA=2AN可知OA:ON=2:3,设A(a,b),可用a、b表示出N点坐标,设点B($\frac{3}{2}$a,y),点A与点B都在反比例函数y=$\frac{k}{x}$的图象上可用a、b表示出B点坐标,再由OA=2AN,△OAB的面积是5可得出△NAB的面积,△ONB的面积,故可得出ab的值,进而得出k的值.
解答 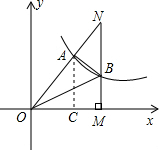 解:过点A作AC⊥x轴于点C,则AC∥MN,
解:过点A作AC⊥x轴于点C,则AC∥MN,
∴△OAC∽△OMN,
∴OC:OM=AC:MN=OA:ON,
∵OA=2AN,即OA:ON=2:3,
∵设A(a,b),
∴OC=a,AC=b,
∴OM=$\frac{3}{2}$a,MN=$\frac{3}{2}$b,
∴N点坐标为($\frac{3}{2}$a,$\frac{3}{2}$b),
设点B($\frac{3}{2}$a,y),
∵点A与点B都在反比例函数y=$\frac{k}{x}$的图象上,
∴k=ab=$\frac{3}{2}$a•y,
∴y=$\frac{2}{3}$b,即B($\frac{3}{2}$a,$\frac{2}{3}$b),
∵OA=2AN,△OAB的面积是10,
∴△NAB的面积是5,
∴△ONB的面积=10+5=15,
∴$\frac{1}{2}$NB•OM=15,$\frac{1}{2}$×($\frac{3}{2}$b-$\frac{2}{3}$b)×$\frac{3}{2}$a=15,
∴ab=24,
∴k=24.
故答案为:24.
点评 本题考查的是反比例函数综合题,涉及到相似三角形的判定与性质、用待定系数法求反比例函数的解析式、反比例函数图象上点的坐标特点等知识,难度适中.

| A. | 2元 | B. | 2.5元 | C. | 3元 | D. | 5元 |
| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=8 | D. | 直线x=-8 |
 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )| A. | 点E | B. | 点F | C. | 点P | D. | 点Q |
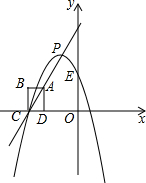 如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.
如图,在平面直角坐标系中,边长为1的正方形ABCD的顶点A在直线y=2x+4上,点B在第二象限,C,D两点均在x轴上,且点C在点D的左侧,抛物线y=-(x-m)2+n的顶点P在直线y=2x+4上运动,且这条抛物线交y轴于点E.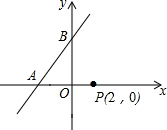 如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.
如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4. 如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);
如图,抛物线y=$\frac{1}{2}{x^2}$+bx+2与y轴交于点C,与x轴交于点A(1,0)和点B(点B在点A右侧);