题目内容
17.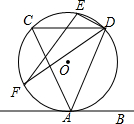 如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
如图,直线AB与⊙O相切于点A,弦CD∥AB,E,F为圆上的两点,且∠CDE=∠ADF,若⊙O的直径为5,CD=4,则弦EF的长为2$\sqrt{5}$.
分析 首先连接OA,并反向延长交CD于点H,连接OC,由直线AB与⊙O相切于点A,弦CD∥AB,可求得OH的长,然后由勾股定理求得AC的长,又由∠CDE=∠ADF,可证得EF=AC,继而求得答案.
解答 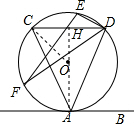 解:连接OA,并反向延长交CD于点H,连接OC,
解:连接OA,并反向延长交CD于点H,连接OC,
∵直线AB与⊙O相切于点A,
∴OA⊥AB,
∵弦CD∥AB,
∴AH⊥CD,
∴CH=$\frac{1}{2}$CD=$\frac{1}{2}$×4=2,
∵⊙O的半径为$\frac{5}{2}$,
∴OA=OC=$\frac{5}{2}$,
∴OH=$\sqrt{O{C}^{2}-C{H}^{2}}$=$\frac{3}{2}$,
∴AH=OA+OH=$\frac{5}{2}$+$\frac{3}{2}$=4,
∴AC=$\sqrt{A{H}^{2}+C{H}^{2}}$=2$\sqrt{5}$.
∵∠CDE=∠ADF,
∴$\widehat{CE}$=$\widehat{AF}$,
∴$\widehat{EF}$=$\widehat{AC}$,
∴EF=AC=2$\sqrt{5}$.
故答案为2$\sqrt{5}$.
点评 此题考查了切线的性质、圆周角定理、垂径定理以及勾股定理等知识.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
8.“五一”节即将来临,某旅游景点超市用700元购进甲、乙两种商品260个,其中甲种商品比乙种商品少用100元,已知甲种商品单价比乙种商品单价高20%.那么乙种商品单价是( )
| A. | 2元 | B. | 2.5元 | C. | 3元 | D. | 5元 |
2. 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )| A. | 点E | B. | 点F | C. | 点P | D. | 点Q |
6.下列四个命题,其中真命题有( )
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
(1)有理数乘以无理数一定是无理数;
(2)顺次联结等腰梯形各边中点所得的四边形是菱形;
(3)在同圆中,相等的弦所对的弧也相等;
(4)如果正九边形的半径为a,那么边心距为a•sin20°.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.在△ABC中,AB=BC=AC=6,则△ABC的面积为( )
| A. | 9 | B. | 18 | C. | 9$\sqrt{3}$ | D. | 18$\sqrt{3}$ |
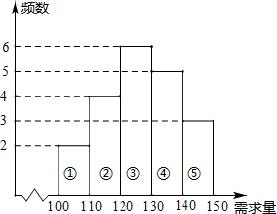 经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.
经销商经销某种农产品,在一个销售月内,每售出1吨该产品获利500元,未售出的产品,每1吨亏损300元.根据历史资料记载的20个月的销售情况,得到如图所示的销售月内市场需求量的频数分布直方图.经销商为下一个销售月购进了130吨该农产品,以x(单位:吨,100≤x≤150)表示下一个销售月内的市场需求量,T(单位:元)表示下一个销售月内经销该农产品的利润.