题目内容
10.若A(-$\frac{3}{2}$,y1)、B($\frac{2}{5}$,y2)是二次函数y=-(x-1)2+$\sqrt{3}$图象上的两点,则y1<y2(填“>”或“<”或“=”).分析 直接计算自变量为-$\frac{3}{2}$和$\frac{2}{5}$所对应的函数值,然后比较函数值的大小即可.
解答 解:∵A(-$\frac{3}{2}$,y1)、B($\frac{2}{5}$,y2)是二次函数y=-(x-1)2+$\sqrt{3}$图象上的两点,
∴y1=-(-$\frac{3}{2}$-1)2+$\sqrt{3}$=-$\frac{25}{4}$+$\sqrt{3}$,y2=-($\frac{2}{5}$-1)2+$\sqrt{3}$=-$\frac{9}{25}$+$\sqrt{3}$,
∴y1<y2.
故答案为<.
点评 本题考查了二次函数图象上点的坐标特征:二次函数图象上的点的坐标满足其解析式.解决本题的关键是把A点和B点坐标代入抛物线解析式求出y1和y2.

练习册系列答案
相关题目
18.抛物线y=x2-8x-1的对称轴为( )
| A. | 直线x=4 | B. | 直线x=-4 | C. | 直线x=8 | D. | 直线x=-8 |
2. 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
 如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )
如图,在数轴上表示数$\frac{\sqrt{5}}{5}$×(-5)的点可能是( )| A. | 点E | B. | 点F | C. | 点P | D. | 点Q |
15.化简$\sqrt{\frac{1}{8}}$,其结果是( )
| A. | $\frac{1}{4}$ | B. | $\frac{{\sqrt{8}}}{8}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | ±$\frac{{\sqrt{2}}}{4}$ |
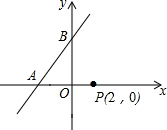 如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.
如图,在平面直角坐标系中,点P的坐标为(2,0),直线y=$\frac{4}{3}$x+4与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM的最小值为4.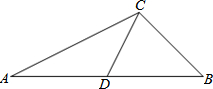 如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值.
如图,在△ABC中,CD是边AB上的中线,∠B是锐角,且sinB=$\frac{{\sqrt{2}}}{2}$,tanA=$\frac{1}{2}$,BC=2$\sqrt{2}$,求边AB的长和cos∠CDB的值.