题目内容
16．
如图，在矩形ABCD中，点F在CB的延长线上，AF=AC，求证：四边形AFBD是平行四边形．
分析 由矩形ABCD的性质，得出AD∥FB，AD=BC，AB⊥FC，再由等腰三角形的性质得到AD=FB，进而推出结论．
解答 ∵四边形ABCD矩形，
∴AD∥FB，AD=BC，AB⊥FC，
∵AF=AC，
∴FB=BC，
∴AD=FB，
∴四边形AFBD是平行四边形．
点评 本题主要考查了平行四边形的性质和判定，等腰三角形的性质，熟记平行四边形的判定和性质是解题的关键．
练习册系列答案
名师金手指领衔课时系列答案
相关题目
6．等腰三角形底边的长为8cm，周长为18cm，则该三角形底边上的高为（ ）
| A． | 6cm | B． | 5cm | C． | 4cm | D． | 3cm |
7．
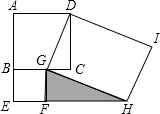如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（ ）
如图为两正方形ABCD、BEFG和矩形DGHI的位置图，其中G、F两点分别在BC、EH上．若AB=5，BG=3，则△GFH的面积为何？（ ）| A． | 10 | B． | 11 | C． | $\frac{15}{2}$ | D． | $\frac{45}{4}$ |
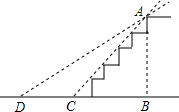某公园在一个斜坡上计划修建台阶，以方便游客，已知斜坡的高AB=12米，斜坡的坡角∠ACB=45°，后来考虑到有老年人的行走方便，决定将坡角改为30°（即∠ADB=30°），请求出CD的长度（精确到0.1米，其中$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）
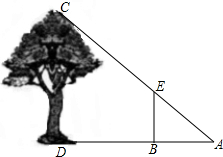如图，某人在点A处测量树高，点A到树的距离AD为21米，将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面，此时，观察视线恰好经过标杆顶点E及树的顶点C，求树CD的高．
5．
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）
如图，底面半径为1，高为$\sqrt{15}$的圆锥，侧面展开后成扇形，以扇形半径中点连线为边作矩形，其他两个顶点在弧上，则矩形的面积是（ ）| A． | 4$\sqrt{5}$-4 | B． | 4$\sqrt{7}$-4 | C． | 8$\sqrt{2}$-4 | D． | 8-2$\sqrt{2}$ |