题目内容
11.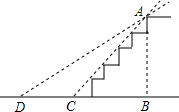 某公园在一个斜坡上计划修建台阶,以方便游客,已知斜坡的高AB=12米,斜坡的坡角∠ACB=45°,后来考虑到有老年人的行走方便,决定将坡角改为30°(即∠ADB=30°),请求出CD的长度(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
某公园在一个斜坡上计划修建台阶,以方便游客,已知斜坡的高AB=12米,斜坡的坡角∠ACB=45°,后来考虑到有老年人的行走方便,决定将坡角改为30°(即∠ADB=30°),请求出CD的长度(精确到0.1米,其中$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 利用坡角的定义得出BC的长,再利用锐角三角函数关系得出BD的长,即可得出答案.
解答 解:由题意可得:AB=BC=12m,则tan30°=$\frac{AB}{BD}$=$\frac{12}{BD}$=$\frac{\sqrt{3}}{3}$,
解得:BD=12$\sqrt{3}$≈20.8(m),
故DC=BD-BC=20.8-12=8.8(m),
答:CD的长度为8.8m.
点评 此题主要考查了解直角三角形的应用,根据题意得出BD的长是解题关键.

练习册系列答案
相关题目
1.已知直角三角形的周长为$4+\sqrt{26}$,斜边为4,则该三角形的面积是( )
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{5}{4}$ |
2.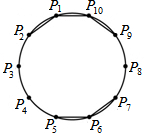 如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
 如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )| A. | P2P3 | B. | P4P5 | C. | P7P8 | D. | P8P9 |
19.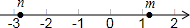 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
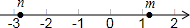 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |
6.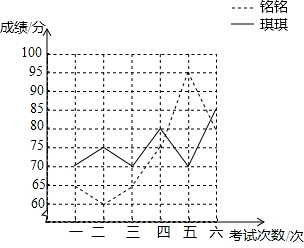 铭铭和琪琪的6次生物考试成绩的折线统计图如图所示.
铭铭和琪琪的6次生物考试成绩的折线统计图如图所示.
(1)请根据图示6次生物考试成绩填写下表:
(2)请你对这两位同学的6次考试成绩进行分析,判断哪位同学的成绩较稳定?
 铭铭和琪琪的6次生物考试成绩的折线统计图如图所示.
铭铭和琪琪的6次生物考试成绩的折线统计图如图所示.(1)请根据图示6次生物考试成绩填写下表:
| 平均数 | 众数 | 中位数 | 方差 | |
| 铭铭 | 75 | 75 | 75 | 125 |
| 琪琪 | 75 | 70 | 72.5 | 33.3 |
 如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.
如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.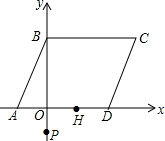 如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.
如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.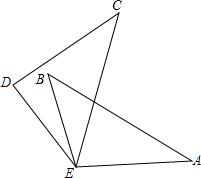 如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.
如图,已知△EAB≌△DCE,AB、EC分别是两个三角形的最长边,∠A=∠C=35°,∠CDE=100°,∠DEB=10°,求∠AEC的度数.