题目内容
8.为迎接“文明城”的检查,某区计划在公共场所安置温馨提示牌和垃圾箱,已知购买5个温馨提示牌和6个垃圾箱共需730元,购买7个温馨提示牌和12个垃圾箱共需1310元.问:(1)购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果该区购买温馨提示牌数量是垃圾箱数的2倍,且所需费用不超过1500元,则最多购买温馨提示牌和垃圾箱数各多少个?
分析 (1)先设安装1个温馨提示牌需要x元,1个垃圾箱需要y元,根据安装5个温馨提示牌和6个垃圾箱需730元,安装7个温馨提示牌和12个垃圾箱需1310元,列出方程组,求出方程组的解即可.
(2)设买垃圾箱m个,则购买温馨提示牌2m个,根据题意得:80m+50•2m≤1500,解得:m$≤\frac{25}{3}$,因为m为正整数,所以m的最大值为8,即可解答.
解答 解:(1)设购买1个温馨提示牌需x元,购买1个垃圾箱需y元,根据题意得:
$\left\{\begin{array}{l}{5x+6y=730}\\{7x+12y=1310}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=50\\}\\{y=80}\end{array}\right.$
答:购买1个温馨提示牌需50元,购买1个垃圾箱需80元.
(2)设买垃圾箱m个,则购买温馨提示牌2m个,根据题意得:
80m+50•2m≤1500,
解得:m$≤\frac{25}{3}$,
∵m为正整数,
∴m的最大值为8,
2×8=16(个),
∴最多购买温馨提示牌16个,垃圾箱数8个.
点评 本题考查了一次函数的实际运用,不等式组的实际运用,二元一次方程组的应用,关键是读懂题意,找出题目中的数量关系,根据数量关系解决问题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
18. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
19.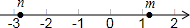 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
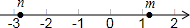 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |
 如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.
如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.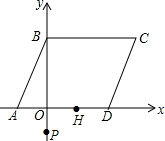 如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.
如图,?ABCD中,A(-2,0)、B(0,4),AD在x轴上,且OD=2OA.