题目内容
7.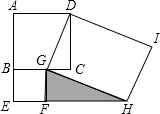 如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?( )
如图为两正方形ABCD、BEFG和矩形DGHI的位置图,其中G、F两点分别在BC、EH上.若AB=5,BG=3,则△GFH的面积为何?( )| A. | 10 | B. | 11 | C. | $\frac{15}{2}$ | D. | $\frac{45}{4}$ |
分析 由四边形ABCD,BEFG是正方形,得到BC=CD=AB=5,GF=BG=3,∠C=∠BGF=∠GFE=∠CGF=∠GFH=90°,根据四边形DGHI是矩形,得到∠DGH=90°,于是得到∠DGC=∠FGH,推出△DGC∽△HGF,得到比例式,求得FH的长度,代入三角形的面积公式即可求出结果.
解答 解:∵四边形ABCD,BEFG是正方形,
∴BC=CD=AB=5,GF=BG=3,∠C=∠BGF=∠GFE=∠CGF=∠GFH=90°,
∵四边形DGHI是矩形,
∴∠DGH=90°,
∴∠DGC+∠CGH=∠FGH+∠HGC=90°,
∴∠DGC=∠FGH,
∴△DGC∽△HGF,
∴$\frac{DC}{FH}$=$\frac{CG}{GF}$,
∴FH=$\frac{CD•GF}{CG}$=$\frac{5×3}{2}$=$\frac{15}{2}$,
∴S△FHG=$\frac{1}{2}$GF•FH=$\frac{45}{4}$,
故选D.
点评 本题考查了正方形的性质,矩形的性质,相似三角形的判定和性质,三角形的面积,掌握定理是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
17. 如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
 如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )
如图,A、B、C、D在⊙O上,BC是⊙O的直径.若∠D=36°,则∠BCA的度数是( )| A. | 72° | B. | 54° | C. | 45° | D. | 36° |
18. 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
 已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )
已知点A、B分别在反比例函数y=$\frac{1}{x}$(x>0),y=-$\frac{3}{x}$(x>0)的图象上,且∠AOB=90°,则∠A为( )| A. | 30° | B. | 45° | C. | 60° | D. | 75° |
2.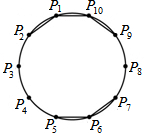 如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
 如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )
如图是P1、P2、…、P10十个点在圆上的位置图,且此十点将圆周分成十等分.今小玉连接P1P2、P1P10、P9P10、P5P6、P6P7,判断小玉再连接下列哪一条线段后,所形成的图形不是轴对称图形?( )| A. | P2P3 | B. | P4P5 | C. | P7P8 | D. | P8P9 |
19.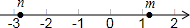 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
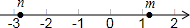 如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )
如图,点M、N在数轴上表示的数分别是m,n,则下列式子中成立的是( )| A. | m-n>0 | B. | |n|-|m|<0 | C. | m+3<n+3 | D. | -m>-n |
 如图,Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线,AC=8,DC=$\frac{1}{2}$AD,则D到AB的距离为$\frac{8}{3}$.
如图,Rt△ABC中,∠ACB=90°,BD是∠ABC的角平分线,AC=8,DC=$\frac{1}{2}$AD,则D到AB的距离为$\frac{8}{3}$. 如图,△ABC与△DEF是一副具有一个内角分别为45°和30°直角三角板的拼图,A、E、C、D在同一条线上.
如图,△ABC与△DEF是一副具有一个内角分别为45°和30°直角三角板的拼图,A、E、C、D在同一条线上. 如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.
如图,在矩形ABCD中,点F在CB的延长线上,AF=AC,求证:四边形AFBD是平行四边形.