题目内容
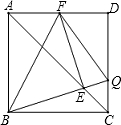 已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为
已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为考点:全等三角形的判定与性质,正方形的性质
专题:
分析:连接DE,延长DA至G,使得AG=CQ,连接BG,证出△BAE≌△DAE,推出BE=DE,∠ADE=∠ABE,求出△FEB是等腰直角三角形,推出∠EBF=45°,证出△GAB≌△QCB,推出BG=BQ;∠ABG=∠CBQ,求出∠GBF=∠QBF,证△GBF≌△QBF,推出QF=GF=AG+AF=CQ+AF,求出△DFQ周长=DF+DQ+QF=2AB=4即可.
解答: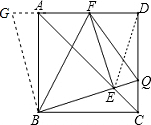
解:如图所示,连接DE,
∵正方形ABCD,
∴AB=AD;∠BAE=∠DAE=45°,∠BAD=90°
在△BAE和△DAE中,
,
∴△BAE≌△DAE(SAS),
∴BE=DE,∠ADE=∠ABE,
∵EF⊥BQ,
∴∠FEB=∠BAD=90°,
∴∠ABE+∠AFE=180°,
∵∠AFE+∠DFE=180°,
∴∠DFE=∠ABE=∠ADE,
∴EF=DE,
∵DE=BE,
∴EF=BE,
即△FEB是等腰直角三角形,
∴∠EBF=45°,
∴∠ABF+∠CBQ=45°,
延长DA至G,使得AG=CQ,
在△GAB和△QCB中
∴△GAB≌△QCB(SAS),
∴BG=BQ;∠ABG=∠CBQ,
∴∠GBF=∠ABG+∠ABF=∠ABF+∠CBQ=45°=∠QBF,
在△GBF和△QBF中
∴△GBF≌△QBF(SAS),
∴QF=GF=AG+AF=CQ+AF,
∴△DFQ周长=DF+DQ+QF=DF+DQ+AF+CQ=AD+DC=2AB=4,
故答案为:4.

解:如图所示,连接DE,
∵正方形ABCD,
∴AB=AD;∠BAE=∠DAE=45°,∠BAD=90°
在△BAE和△DAE中,
|
∴△BAE≌△DAE(SAS),
∴BE=DE,∠ADE=∠ABE,
∵EF⊥BQ,
∴∠FEB=∠BAD=90°,
∴∠ABE+∠AFE=180°,
∵∠AFE+∠DFE=180°,
∴∠DFE=∠ABE=∠ADE,
∴EF=DE,
∵DE=BE,
∴EF=BE,
即△FEB是等腰直角三角形,
∴∠EBF=45°,
∴∠ABF+∠CBQ=45°,
延长DA至G,使得AG=CQ,
在△GAB和△QCB中
|
∴△GAB≌△QCB(SAS),
∴BG=BQ;∠ABG=∠CBQ,
∴∠GBF=∠ABG+∠ABF=∠ABF+∠CBQ=45°=∠QBF,
在△GBF和△QBF中
|
∴△GBF≌△QBF(SAS),
∴QF=GF=AG+AF=CQ+AF,
∴△DFQ周长=DF+DQ+QF=DF+DQ+AF+CQ=AD+DC=2AB=4,
故答案为:4.
点评:本题考查了正方形的性质,全等三角形的性质和判定的应用,题目比较好,综合性比较强.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
要判断甲、乙两队舞蹈队的身高哪队比较整齐,通常需要比较这两队舞蹈队身高的( )
| A、方差 | B、中位数 |
| C、众数 | D、平均数 |
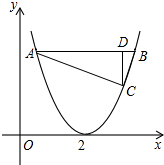 如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )
如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )| A、CD=1 |
| B、1<CD<2 |
| C、CD=2 |
| D、随着A点变化而变化 |
若实数a<1,则实数M=a,N=
,P=
的大小关系为( )
| a+2 |
| 3 |
| 2a+1 |
| 3 |
| A、P>N>M |
| B、M>N>P |
| C、N>P>M |
| D、M>P>N |
在同一坐标系中,作函数y=3x2,y=-3x2,y=
x2的图象,它们的共同特点是( )
| 1 |
| 3 |
| A、都是关于x轴对称,抛物线开口向上 |
| B、都是关于y轴对称,抛物线的顶点都是原点 |
| C、都是关于原点对称,抛物线的顶点都是原点 |
| D、都是关于y轴对称,抛物线开口向下 |
 如图,已知AB=3,CD=5,E为BC中点,F为AD中点,则EF=
如图,已知AB=3,CD=5,E为BC中点,F为AD中点,则EF=