题目内容
 如图,已知AB=3,CD=5,E为BC中点,F为AD中点,则EF=
如图,已知AB=3,CD=5,E为BC中点,F为AD中点,则EF=考点:全等三角形的判定与性质,三角形中位线定理
专题:
分析:连接AE并延长交CD于M,可证得△BEA≌△CEM,可得DM的长,且E为AM的中点,所以EF为△AMD的中位线,可求得EF.
解答: 解:如图所示,连接AE并延长交CD于M,
解:如图所示,连接AE并延长交CD于M,
∵AB∥CD,E是BC的中点,
在△ABE和△CEM中
∴△BEA≌△CEM(ASA),
∴AB=CM=3,AE=ME,
∴DM=CD-CM=2,E是AM的中点
又∵F是AD的中点,
∴EF是△AMD的中位线,
∴EF=
DM=1.
故答案为:1.
 解:如图所示,连接AE并延长交CD于M,
解:如图所示,连接AE并延长交CD于M,∵AB∥CD,E是BC的中点,
在△ABE和△CEM中
|
∴△BEA≌△CEM(ASA),
∴AB=CM=3,AE=ME,
∴DM=CD-CM=2,E是AM的中点
又∵F是AD的中点,
∴EF是△AMD的中位线,
∴EF=
| 1 |
| 2 |
故答案为:1.
点评:本题主要考查三角形全等的判定及性质,构造全等三角形,证明EF为三角形的中位线是解题的关键.

练习册系列答案
相关题目
已知一个等腰三角形底边的长为5cm,一腰上的中线把其周长分成的两部分的差为3cm,则腰长为( )
| A、2cm | B、8cm |
| C、2cm或8cm | D、10cm |
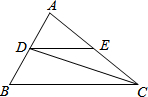 如图,已知△ABC中,∠C的平分线交AB于点D,过D作BC的平行线交AC于E,若AC=6,BC=12,求DE的长.
如图,已知△ABC中,∠C的平分线交AB于点D,过D作BC的平行线交AC于E,若AC=6,BC=12,求DE的长.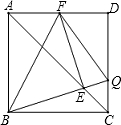 已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为
已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为 小丽从A地前往B地,到达后立刻返回.她与A地的距离y(千米)和所用时间x(小时)之间的函数关系如图所示.
小丽从A地前往B地,到达后立刻返回.她与A地的距离y(千米)和所用时间x(小时)之间的函数关系如图所示. 线段AB=12cm,D是AB上一点,且AD=8cm,C为AB中点,求线段CD的长度.
线段AB=12cm,D是AB上一点,且AD=8cm,C为AB中点,求线段CD的长度.