题目内容
在同一坐标系中,作函数y=3x2,y=-3x2,y=
x2的图象,它们的共同特点是( )
| 1 |
| 3 |
| A、都是关于x轴对称,抛物线开口向上 |
| B、都是关于y轴对称,抛物线的顶点都是原点 |
| C、都是关于原点对称,抛物线的顶点都是原点 |
| D、都是关于y轴对称,抛物线开口向下 |
考点:二次函数的图象
专题:
分析:本题的三个抛物线解析式都符合y=ax2形式,可以从顶点坐标和对称轴找相同点.
解答:解:因为y=ax2形式的二次函数对称轴都是y轴,且顶点都在原点,
所以它们的共同特点是:关于y轴对称的抛物线,有公共的顶点.
故选:B.
所以它们的共同特点是:关于y轴对称的抛物线,有公共的顶点.
故选:B.
点评:此题主要考查了二次函数图象,要掌握y=ax2形式的二次函数对称轴都是y轴,且顶点都在原点是解题关键.

练习册系列答案
 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
某学校有320名学生,现对他们的生日进行统计(可以不同年)( )
| A、至少有两人生日相同 |
| B、不可能有两人生日相同 |
| C、可能有两人生日相同,且可能性较大 |
| D、可能有两人生日相同,但可能性较小 |
把下列各数填在相应的集合里:
17,-
,-21,0,0.35,-6.28,1,10%,
正整数集合:{ }
负整数集合:{ }
正分数集合:{ }
负分数集合:{ }
整数集合:{ }
有理数集合:{ }.
17,-
| 3 |
| 4 |
| 1 |
| 5 |
正整数集合:{ }
负整数集合:{ }
正分数集合:{ }
负分数集合:{ }
整数集合:{ }
有理数集合:{ }.
已知:a<b,c≠0,那么下列结论一定正确的是( )
| A、a+c>b-c | ||||
| B、ac2<bc2 | ||||
| C、ac<bc | ||||
D、
|
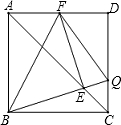 已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为
已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为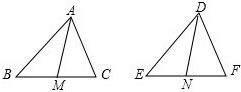 已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.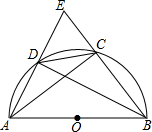 如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD.
如图:AB是半圆的直径,∠ABC的平分线交半圆于D,AD和BC的延长线交于圆外一点E,连结CD. 线段AB=12cm,D是AB上一点,且AD=8cm,C为AB中点,求线段CD的长度.
线段AB=12cm,D是AB上一点,且AD=8cm,C为AB中点,求线段CD的长度.