题目内容
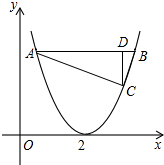 如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )
如图是二次函数y=(x-2)2的图象,点A、B、C是抛物线上3个点,且△ABC为直角三角形,CD⊥AB,则高CD应该满足( )| A、CD=1 |
| B、1<CD<2 |
| C、CD=2 |
| D、随着A点变化而变化 |
考点:二次函数的性质
专题:
分析:根据抛物线解析式求出对称轴,再设点A(a,(a-2)2),B((4-a),(a-2)2),点C(c,(c-2)2),然后判断出点D的坐标,再设出直线AC、BC的解析式,然后把点A、B、C的坐标代入表示出两直线解析式的k值,然后根据两直线互相垂直,k值的乘积为-1用a表示出c,再求出(c-2)2,即可得解.
解答:解:∵二次函数解析式为y=(x-2)2,
∴对称轴为直线x=2,
由图可知,AB∥x轴,
所以,设点A(a,(a-2)2),则B((4-a),(a-2)2),
设点C(c,(c-2)2),
∵CD⊥AB,
∴D(c,(a-2)2),
设直线AC、BC的解析式分别为y=k1x+b1,y=k2x+b2,
将A、B、C的坐标分别代入得
,
,
所以,k1=a+c-4,
k2=c-a,
∵CD⊥AB,
∴k1•k2=(a+c-4)(c-a)=-1,
整理得,c2-4c-a2+4a+1=0,
∴(a-2)2-(c-2)2=1,
∴CD=1,
故高CD应该满足CD=1.
故选A.
∴对称轴为直线x=2,
由图可知,AB∥x轴,
所以,设点A(a,(a-2)2),则B((4-a),(a-2)2),
设点C(c,(c-2)2),
∵CD⊥AB,
∴D(c,(a-2)2),
设直线AC、BC的解析式分别为y=k1x+b1,y=k2x+b2,
将A、B、C的坐标分别代入得
|
|
所以,k1=a+c-4,
k2=c-a,
∵CD⊥AB,
∴k1•k2=(a+c-4)(c-a)=-1,
整理得,c2-4c-a2+4a+1=0,
∴(a-2)2-(c-2)2=1,
∴CD=1,
故高CD应该满足CD=1.
故选A.
点评:本题考查了二次函数的性质,主要利用了二次函数图象上点的坐标特征,一次函数图象上点的坐标特征,两互相垂直的直线解析式的k值的关系.

练习册系列答案
相关题目
对于反比例函数y=
的图象,它在每个象限内( )
| 5 |
| x |
| A、y都取正值 |
| B、y随x的增大而增大 |
| C、y随x的增大而减小 |
| D、y都取负值 |
已知M(a,3)和N(4,b)关于y轴对称,则(a+b)2012的值为( )
| A、1 |
| B、-1 |
| C、72012 |
| D、-72012 |
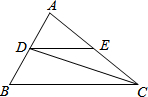 如图,已知△ABC中,∠C的平分线交AB于点D,过D作BC的平行线交AC于E,若AC=6,BC=12,求DE的长.
如图,已知△ABC中,∠C的平分线交AB于点D,过D作BC的平行线交AC于E,若AC=6,BC=12,求DE的长.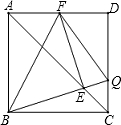 已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为
已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为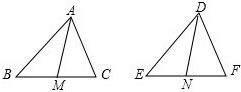 已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.