题目内容
已知抛物线y=ax2+bx+c过第一、二、四象限(不经过原点)与x轴交于A、B两点,与y轴交于点C.
(1)确定a,b,c的符号;
(2)若∠CAO=45°,∠CBO=30°,求证:ac=
;
(3)若∠CAO=45°,∠CBO=30°,且AB=3-
,求抛物线的解析式.
(1)确定a,b,c的符号;
(2)若∠CAO=45°,∠CBO=30°,求证:ac=
| ||
| 3 |
(3)若∠CAO=45°,∠CBO=30°,且AB=3-
| 3 |
考点:抛物线与x轴的交点
专题:计算题
分析:(1)根据二次函数与系数a、b、c的关系求解;
(2)先确定C点坐标得到OC=c,在Rt△OAC中,由于∠CAO=45°,根据等腰直角三角形的性质得OA=OC=c,则A点坐标为(c,0),在Rt△BOC中,由于∠CBO=30°,根据含30度的直角三角形三边的关系得到OB=
OC=
c,则B点坐标为(
c,0),然后利用交点式得到抛物线解析式为y=a(x-c)(x-
c),展开得y=ax2-(1+
)ac+
ac2,与原解析式对比即可得到
ac2=c,所以ac=
;
(3)由(2)得到A点坐标为(c,0),B点坐标为(
c,0),则
c-c=3-
,解得c=
,再利用ac=
得到a=
,然后把a和c的值代入y=ax2-(1+
)ac+
ac2中化简即可.
(2)先确定C点坐标得到OC=c,在Rt△OAC中,由于∠CAO=45°,根据等腰直角三角形的性质得OA=OC=c,则A点坐标为(c,0),在Rt△BOC中,由于∠CBO=30°,根据含30度的直角三角形三边的关系得到OB=
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
(3)由(2)得到A点坐标为(c,0),B点坐标为(
| 3 |
| 3 |
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
解答:(1)解: ∵抛物线y=ax2+bx+c过第一、二、四象限(不经过原点),
∵抛物线y=ax2+bx+c过第一、二、四象限(不经过原点),
∴a>0,b<0,c>0;
(2)证明:C点坐标为(0,c),
在Rt△OAC中,∵∠CAO=45°,
∴OA=OC=c,
∴A点坐标为(c,0),
在Rt△BOC中,∠CBO=30°,
∴OB=
OC=
c,
∴B点坐标为(
c,0),
∴抛物线解析式为y=a(x-c)(x-
c)
=ax2-(1+
)ac+
ac2,
∴
ac2=c,
∴ac=
;
(3)解:∵A点坐标为(c,0),B点坐标为(
c,0),
∴
c-c=3-
,
∴c=
,
而ac=
,
∴a=
,
∴y=
x2-(1+
)•
x+
=
x2-
•x+
.
 ∵抛物线y=ax2+bx+c过第一、二、四象限(不经过原点),
∵抛物线y=ax2+bx+c过第一、二、四象限(不经过原点),∴a>0,b<0,c>0;
(2)证明:C点坐标为(0,c),
在Rt△OAC中,∵∠CAO=45°,
∴OA=OC=c,
∴A点坐标为(c,0),
在Rt△BOC中,∠CBO=30°,
∴OB=
| 3 |
| 3 |
∴B点坐标为(
| 3 |
∴抛物线解析式为y=a(x-c)(x-
| 3 |
=ax2-(1+
| 3 |
| 3 |
∴
| 3 |
∴ac=
| ||
| 3 |
(3)解:∵A点坐标为(c,0),B点坐标为(
| 3 |
∴
| 3 |
| 3 |
∴c=
| 3 |
而ac=
| ||
| 3 |
∴a=
| 1 |
| 3 |
∴y=
| 1 |
| 3 |
| 3 |
| ||
| 3 |
| 3 |
=
| 1 |
| 3 |
3+
| ||
| 3 |
| 3 |
点评:本题考查了抛物线与x轴的交点:二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.也考查了二次函数的性质.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
对于反比例函数y=
的图象,它在每个象限内( )
| 5 |
| x |
| A、y都取正值 |
| B、y随x的增大而增大 |
| C、y随x的增大而减小 |
| D、y都取负值 |
已知一个等腰三角形底边的长为5cm,一腰上的中线把其周长分成的两部分的差为3cm,则腰长为( )
| A、2cm | B、8cm |
| C、2cm或8cm | D、10cm |
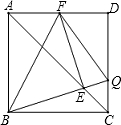 已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为
已知正方形ABCD中,Q是CD上一点,BQ交AC于点E,EF⊥BQ交AD于点F,连接FQ、BF,若AB=2,则△DFQ周长为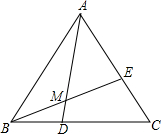 如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=
如图,D为△ABC中BC上一点,E为AC上一点,连接AD,BE交于点M,满足AM:MD=3:1,BD:DC=2:3,则AE:EC=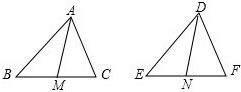 已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.
已知:△ABC和△DEF中,AB=DE,BC=EF,AM是△ABC的中线,DN是△DEF的中线,AM=DN,求证:△ABC≌△DEF.