题目内容
2.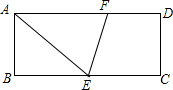 如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )
如图,在矩形ABCD中,E为BC边的中点,∠AEC的平分线交AD边于点F,若AB=3,AD=8,则FD的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据矩形点的性质可得AD∥BC,AD=BC,再求出BE的长度,再根据勾股定理列式求出AE的长,然后根据角平分线的定义求出∠AEF=∠CEF,根据两直线平行,内错角相等求出∠AFE=∠CEF,再求出AEF=∠AFE,根据等角对等边可得AE=AF,然后根据FD=AD-AF代入数据计算即可得解.
解答 解:在矩形ABCD中,AD∥BC,AD=BC=8,
∵E为BC的中点,
∴BE=$\frac{1}{2}$BC=$\frac{1}{2}$×8=4,
在Rt△ABE中,AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵EF是∠AEC的角平分线,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠AFE=∠CEF,
∴∠AEF=∠AFE,
∴AE=AF,
∴FD=AD-AF=8-5=3.
故选:C.
点评 本题考查了矩形的性质,勾股定理的应用,两直线平行,内错角相等的性质,等角对等边的性质,熟记相关性质是解题关键.

练习册系列答案
相关题目
12.甲、乙两个城市,乙城市位于甲城市北偏东30°方向,距离为80km,那么甲城市位于乙城市( )
| A. | 南偏东30°方向,距离为80km | B. | 南偏西30°方向,距离为80km | ||
| C. | 南偏东60°方向,距离为80km | D. | 南偏西60°方向,距离为80km |
13. 如图,AB∥CD,EF⊥AB于E,EF交CD于F,己知∠2=20°,则∠1等于( )
如图,AB∥CD,EF⊥AB于E,EF交CD于F,己知∠2=20°,则∠1等于( )
 如图,AB∥CD,EF⊥AB于E,EF交CD于F,己知∠2=20°,则∠1等于( )
如图,AB∥CD,EF⊥AB于E,EF交CD于F,己知∠2=20°,则∠1等于( )| A. | 30° | B. | 50° | C. | 70° | D. | 45° |
10.下列命题的逆命题是真命题的是( )
| A. | 若a=b,则a2=b2 | B. | 全等三角形的周长相等 | ||
| C. | 若a=0,则ab=0 | D. | 有两边相等的三角形是等腰 |
17.两个相似三角形对应高的长分别为8cm和6cm,则它们的面积比为( )
| A. | 4:3 | B. | $\sqrt{3}$:2 | C. | 2:$\sqrt{3}$ | D. | 16:9 |
14.矩形具有而菱形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线垂直 | D. | 每一条对角线平分一组对角 |
11.一元一次不等式组$\left\{\begin{array}{l}{x>a}\\{x<b}\end{array}\right.$无解,则a与b的关系是( )
| A. | a≥b | B. | a≤b | C. | a>b>0 | D. | a<b<0 |
 如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.
如图,在直角坐标系中,过点P(x,0)作x轴的垂线分别交抛物线y=x2+2与直线y=-$\frac{1}{2}$x于A,B两点,以线段AB为对角线作正方形ADBC,已知点Q(a,b)为该抛物线上的点.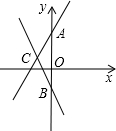 如图,已知直线y=2x+4与直线y=-2x-2相交于点C.
如图,已知直线y=2x+4与直线y=-2x-2相交于点C.