题目内容
4.下列命题:①对角线相等的四边形是矩形;
②如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形一定是正方形;
③用配方法解方程x2-4x=5时,此方程可变形为(x-2)2=9;
④已知数据x1,x2,x3的平均数为$\overline{x}$,则数据x1+2,x2+2,x3+2的平均数为$\overline{x}$+2.
其中真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据矩形的判定、三角形中位线定理和正方形的判定、配方法以及平均数的规律分别判断即可.
解答 解:①对角线互相平分且相等的四边形是矩形;故①是假命题;
②如果顺次连接一个四边形各边中点得到的是一个正方形,那么原四边形不一定是正方形;顾②是假命题;
③用配方法解方程x2-4x=5时,此方程可变形为(x-2)2=9;故③是真命题;
④已知数据x1,x2,x3的平均数为$\overline{x}$,则数据x1+2,x2+2,x3+2的平均数为$\overline{x}$+2;故④是真命题.
其中真命题的个数有2个,故选:B.
点评 本题考查了命题与定理、矩形的判定、为矩形中位线定理、正方形的判定、配方法以及平均数;解题的关键是熟记矩形和正方形的判定、配方法和平均数规律,难度不大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.矩形具有而菱形不具有的性质是( )
| A. | 对角线互相平分 | B. | 对角线相等 | ||
| C. | 对角线垂直 | D. | 每一条对角线平分一组对角 |
15.下列图案中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
19.以下列长度的各组线段为边,不能构成三角形的是( )
| A. | 3,4,8 | B. | 15,20,8 | C. | 9,15,8 | D. | 4,9,6 |
4.-64的立方根是( )
| A. | ±8 | B. | 4 | C. | -4 | D. | 16 |
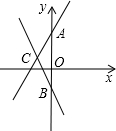 如图,已知直线y=2x+4与直线y=-2x-2相交于点C.
如图,已知直线y=2x+4与直线y=-2x-2相交于点C. 已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF.
已知:如图,在矩形ABCD中,AB=3,点E在AB的延长线上,且AE=AC,联结CE,取CE的中点F,联结BF、DF. 如图,已知两条直线l1、l2的交点可看作是某方程组的解,则这个方程组为$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{3}{2}}\\{y=\frac{3}{2}x}\end{array}\right.$.
如图,已知两条直线l1、l2的交点可看作是某方程组的解,则这个方程组为$\left\{\begin{array}{l}{y=\frac{3}{4}x+\frac{3}{2}}\\{y=\frac{3}{2}x}\end{array}\right.$.