题目内容
20.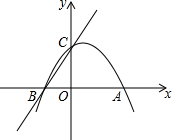 如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).
如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).(1)求二次函数解析式,并写出顶点坐标;
(2)令直线BC的解析式为y2,分析并观察图象,直接写出当y1<y2时,x的取值范围.
分析 (1)把A点和C点坐标分别代入y1=-x2+nx+m中得到关于m、n的方程组,然后解方程组求出m和n的值即可得到二次函数解析式,再把解析式配成顶点式得到顶点坐标;
(2)根据抛物线与x轴的交点问题求出B点坐标,然后观察函数图象,写出直线BC在抛物线上方所对应的自变量的范围即可.
解答 解:(1)把A(3,0),C(0,3)分别代入y1=-x2+nx+m得$\left\{\begin{array}{l}{-9+3n+m=0}\\{m=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{n=2}\\{m=3}\end{array}\right.$,
所以二次函数解析式为y1=-x2+2x+3;
因为y1=-x2+2x+3=-(x-1)2+4,
所以二次函数图象的顶点坐标为(1,4);
(2)当y=0时,-x2+2x+3=0,解得x1=-1,x2=3,则B(-1,0),
所以当x<-1或x>0时,y1<y2.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.二次函数y=ax2+bx+c(a,b,c是常数,a≠0)的交点与一元二次方程ax2+bx+c=0根之间的关系:△=b2-4ac决定抛物线与x轴的交点个数.△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
18.甲、乙两数和为21,甲数的2倍等于乙数的5倍,求甲、乙两数.设甲数为x,乙数为y,则下列方程组正确的是( )
| A. | $\left\{{\begin{array}{l}x+y=21\\ 5x=2y\end{array}}\right.$ | B. | $\left\{{\begin{array}{l}x+y=21\\ 2x=5y\end{array}}\right.$ | C. | $\left\{{\begin{array}{l}2x+5y=21\\ 2x=5y\end{array}}\right.$ | D. | $\left\{{\begin{array}{l}2x+5y=21\\ 5x=2y\end{array}}\right.$ |
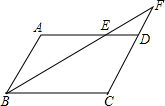 如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.
如图,在平行四边形ABCD中,若AB=6,AD=10,∠ABC的平分线交AD于点E,交CD的延长线于点F,求DF的长.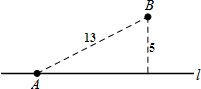 如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
如图,一条笔直的公路l穿过草原,公路边有一消防站A,距离公路5千米的地方有一居民点B,A、B的直线距离是13千米.一天,居民点B着火,消防员受命欲前往救火,若消防车在公路上的最快速度是80千米/小时,而在草地上的最快速度是40千米/小时,则消防车在出发后最快经过$\frac{5\sqrt{3}+12}{80}$小时可到达居民点B.(友情提醒:消防车可从公路的任意位置进入草地行驶.)
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m+4与y轴交于点A(0,3),与x轴交于点B,C(点B在点C左侧).