题目内容
9.在平面直角坐标系中,O为原点,四边形OABC是矩形,点A,C的坐标分别为(3,0),(0,1).点D是边BC上的动点(与端点B,C不重合),过点D作直线y=-$\frac{1}{2}$x+b交边OA于点E.(Ⅰ)如图①,求点D和点E的坐标(用含b的式子表示);
(Ⅱ)如图②,若矩形OABC关于直线DE的对称图形为矩形O1A1B1C1,试探究矩形O1A1B1C1与矩形OABC的重叠部分的面积是否发生变化?若不变,求出重叠部分的面积;若改变,请说明理由;
(Ⅲ)矩形OABC绕着它的对称中心旋转,如果重叠部分的形状是菱形,请直接写出这个菱形的面积的最小值和最大值.
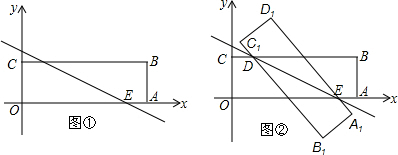
分析 (1)根据题意得出点D纵坐标为1,点E的纵坐标为0,代入解析式即可;
(2)如图根据菱形的性质和勾股定理从而得出结论;
(3)分两种情况得出菱形面积的最大和最小值.
解答 解:(1)∵四边形OABC是矩形,
∴CB∥x轴,
由点A,C的坐标分别为(3,0),(0,1).
可得点D的纵坐标为1,
当y=1时,y=$-\frac{1}{2}x$+b,
解得:x=2b-2,
∴D的坐标为(2b-2,1)
当y=0时,y=$-\frac{1}{2}x$+b,
解得:x=2b,
∴E的坐标为(2b,0)
(Ⅱ)CB与O1A1的交点为M,C1B1与OA的交点为N,如图:
∵四边形OABC,四边形O1A1B1C1是矩形,
∴CB∥OA,C1B1∥O1A1,
∴四边形DMEN是平行四边形,
∵矩形OABC关于直线DE的对称图形为矩形O1A1B1C1,
∴∠1=∠2,
∵CB∥OA,
∴∠2=∠3,
∴∠1=∠3,
∴DM=ME,
∴平行四边形DMEN是菱形,
过点D作DH⊥OA于点H,
由D(2b-2,1),E(2b,0),
可知CD=2b-2,OE=2b,OH=CD=2b-2,
∴EH=OE-OH=2b-(2b-2)=2,
设菱形DMEN的边长为m,
在Rt△DHN中,DH=1,HN=EH-NE=2-m,DN=m,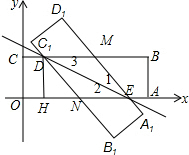
由DH2+HN2=DN2,得12+(2-m)2=m2,
解得:m=$\frac{5}{4}$,
∴${S}_{菱形DMEN}=NE•DH=\frac{5}{4}×1=\frac{5}{4}$,
所以重叠部分菱形DMEN的面积不变,为$\frac{5}{4}$;
(Ⅲ)当NE=1时,菱形面积的最小值是1;
当NE=$\frac{5}{3}$时,菱形面积的最大值是$\frac{5}{3}$.(D与C重合,A与E重合,设DN=AN=x,在Rt△DNO中利用勾股定理列出方程计算)
点评 本题考查了一次函数的性质,关键是根据点在函数图象上,点的坐标满足函数的解析式.也利用了菱形的特点.

 名校课堂系列答案
名校课堂系列答案 如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )
如图,直线m∥n,BA⊥AC于A点,AB、AC分别交直线n于点B、C,∠2=55°,则∠1的度数是( )| A. | 50° | B. | 45° | C. | 35° | D. | 30° |
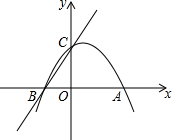 如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3).
如图所示,二次函数y1=-x2+nx+m的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C(0,3). 台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南256千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南256千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.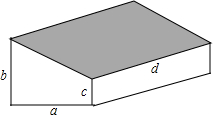 如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?
如图,要修建一个蔬菜大棚,棚的横截面是直角梯形,棚宽a=6米,棚高分别为b=5米,c=2米,长为d=30米,现要在棚顶覆盖塑料膜(即图中阴影部分),求共计需要塑料膜多少平方米?