题目内容
18.将4个数a,b,c,d排成2行、2列,两边各加一条竖直线记成$\left|\begin{array}{l}a\\ c\end{array}\right.\left.\begin{array}{l}b\\ d\end{array}\right|$,定义$\left|\begin{array}{l}a\\ c\end{array}\right.\left.\begin{array}{l}b\\ d\end{array}\right|$=$\frac{a}{d}-\frac{b}{c}$,上述记号就叫做2阶行列式.则$\left|\begin{array}{l}2\\{x^2}-4\end{array}\right.\left.\begin{array}{l}8\\ x-2\end{array}\right|$=$\frac{2}{x+2}$.分析 原式利用题中的新定义化简,计算即可得到结果.
解答 解:根据题中的新定义得:$\frac{2}{x-2}$-$\frac{8}{{x}^{2}-4}$=$\frac{2(x+2)-8}{(x+2)(x-2)}$=$\frac{2(x-2)}{(x+2)(x-2)}$=$\frac{2}{x+2}$.
故答案为:$\frac{2}{x+2}$
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.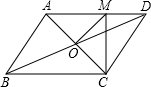 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
 如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )
如图,?ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M,如果△CDM的周长是40cm,则平行四边形ABCD的周长是( )| A. | 40cm | B. | 60cm | C. | 70cm | D. | 80cm |
3.下列各式计算正确的是( )
| A. | a3+a4=a7 | B. | (3a+b)2=9a2+b2 | C. | (-ab3)2=a2b6 | D. | a6b÷a2=a3b |
8.函数y=$\frac{3}{\sqrt{x+2}}$中,自变量x的取值范围是( )
| A. | x≠-2 | B. | x≥-2 | C. | x>-2 | D. | x>2 |
 如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.
如图,给一幅长8m,宽5m的矩形风景画(图中阴影部分)镶一个画框,若设画框的宽均为xm,装好画框后总面积为70m2,则根据题意可列方程为(8+2x)(5+2x)=70.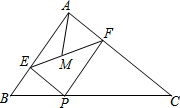 如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.
如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是$\frac{12}{5}$.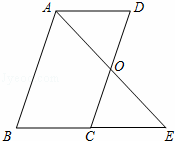 已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.
已知:?ABCD中,E是CD的中点,AE的延长线与BC的延长线相交于点F.求证:BC=CF.