题目内容
8.已知直线y=$\frac{1}{2}$x+m与x轴交于点A,与y轴交于点C,抛物线y=-$\frac{1}{2}$x2+bx+3过A、C两点,交x轴另一点B.(1)如图1,求抛物线的解析式;
(2)如图2,P、Q两点在第二象限的抛物线上,且关于对称轴对称,点F为线段AP上一点,2∠PQF+∠PFQ=90°,射线QF与过点A且垂直x轴的直线交于点E,AP=QE,求PQ长;
(3)如图3,在(2)的条件下,点D在QP的延长线上,DP:DQ=1:4,点K为射线AE上一点连接QK,过点D作DM⊥QK垂足为M,延长DM交AB于点N,连接AM,当∠AMN=45°时,过点A作AR⊥DN交抛物线于点R,求R点坐标.
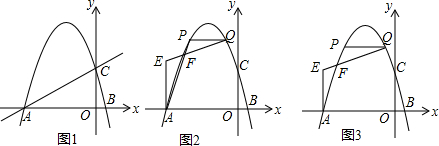
分析 (1)先求点C的坐标,接着求出一次函数的解析式,进而可得A点坐标,然后将A点坐标代入二次函数解析式即可求出b;
(2)由于P、Q关于抛物线对称轴对称,故PQ与x轴平行,所以只需求P、Q横坐标即可求出PQ长度.延长QP、AE交于点H,易证△HAP≌QEH,从而QH=AH,过点Q作QK⊥AB于点G,则四边形AGQH是正方形,设出Q点坐标,利用QH=QG建立方程即可求出P、Q两点坐标,从而得出答案;
(3)在(2)的条件下,过点A作AG⊥AM交DN延长线于点G,易证△AKM≌△ANG,从而AK=AN,过点D作DL⊥AB于点L,则四边形HALD是矩形,易得△HKQ≌△LND,进而求得HK=LN=2,设出R点坐标,由tan∠HQK=tan∠OAR=$\frac{HK}{HQ}=\frac{2}{5}$建立方程即可求出R点坐标.
解答 解:(1)∵当x=0时,$y=-\frac{1}{2}{x}^{2}+bx+3=3$,
∴C(0,3),
将点C代入$y=\frac{1}{2}x+m$得m=3,
当y=0时,x=-6,
∴A(-6,0),
将点A代入$y=-\frac{1}{2}{x}^{2}+bx+3$得$b=-\frac{5}{2}$,
∴抛物线的解析式为$y=-\frac{1}{2}{x}^{2}-\frac{5}{2}x+3$;
(2)如图2,延长QP、AE交于点H,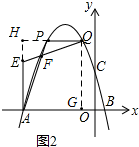
∵点P、Q关于对称轴对称,
∴QP∥x轴,
∵AE⊥x轴,
∴∠H=90°,
∵2∠PQF+∠PFQ=90°,
∴∠PQF+∠PFQ=90°-∠PQF=∠HEQ=∠HAP+∠EFA,
∴∠PQF=∠HAP,
在△HAP和△QEH中,
$\left\{\begin{array}{l}{QE=AP}\\{∠HAP=∠PQF}\\{∠H=∠H}\end{array}\right.$
∴△HAP≌△QEH,
∴QH=AH,
过点Q作QG⊥AB于点G,
∴四边形AGQH是正方形,
设点Q(t,$-\frac{1}{2}{t}^{2}-\frac{5}{2}t+3$),
∴QH=t+6,
QG=$-\frac{1}{2}{t}^{2}-\frac{5}{2}t+3$,
∴t+6=$-\frac{1}{2}{t}^{2}-\frac{5}{2}t+3$,
解得:t=-1或t=-6(舍去),
∴Q(-1,5);
∵点P、Q关于x=-$\frac{5}{2}$对称,
∴点P(-4,5),
∴PQ=3;
(3)∵DP:DQ=1:4,
∴DP=1,D(-5,5),HD=1,
∵DN⊥QK,∠AMN=45°,过点A作AG⊥AM交DN延长线于点G,如图3,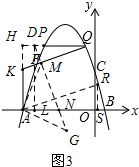
∴AM=AG,
∴KMN+∠KAN=180°,
∴∠MKA+∠MNA=180°,∠ANG+∠MNA=180°,
∴∠MKA=∠ANG,
∵KAN=∠MAG=90°,
∴∠MAK=∠NAG,
在△AKM和△ANG中,
$\left\{\begin{array}{l}{∠MAK=∠NAG}\\{∠MKA=∠ANG}\\{AM=AG}\end{array}\right.$
∴△AKM≌△ANG,
∴AK=AN,
过点D作DL⊥AB于点L,四边形HALD是矩形,
∴HD=AL=1,AH=DL=QH,∠HKQ=∠DNL,
在△HKQ和△LND中,
$\left\{\begin{array}{l}{∠HKQ=∠DNL}\\{QH=DL}\\{∠H=∠DLN}\end{array}\right.$
∴△HKQ≌△LND,
∴HK=LN,
设HK=LN=m,
则AN=AK=m+1,
∴AH=m+1+m=5,
∴m=2,
∵∠HQK=∠OAR,
∴tan∠HQK=tan∠OAR=$\frac{HK}{HQ}=\frac{2}{5}$,
设R(m,-$\frac{1}{2}{m}^{2}-\frac{5}{2}m+3$),
过点R作RS⊥AB于点S,
∴$\frac{-\frac{1}{2}{m}^{2}-\frac{5}{2}m+3}{m+6}=\frac{2}{5}$,
∴m=$\frac{1}{5}$或m=-6(舍),
∴R($\frac{1}{5}$,$\frac{62}{25}$).
点评 本题是二次函数综合题,主要考查了待定系数法求二次函数解析式、全等三角形的判定与性质、一元二次方程序的解法、正方形的判定与性质、矩形的判定与性质、锐角三角形函数等知识点,综合性很强,难度较大.本题主要涉及较多的几何知识,因此熟练掌握全等三角形、相似三角形、特殊四边形等基本几何图形的性质是解答本题的关键.

 阅读快车系列答案
阅读快车系列答案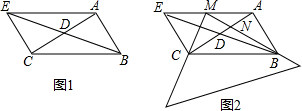
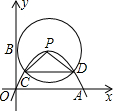 如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).
如图,在平面直角坐标系中,点P在第一象限,以P为顶点的抛物线经过原点,与x轴正半轴相交于点A,⊙P与y轴相切于点B,交抛物线交于点C、点D.若点A的坐标为(m,0),CD=n,则△PCD的周长为m+n(用含m、n的代数式表示).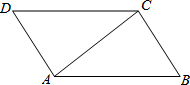 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线. 如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.
如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(-4,0)、点B(0,-8),直线AC与y轴交于点C(0,-4).P是抛物线上A、B两点之间的一点(P不与点A、B重合),过点P作PD∥y轴交直线AC于点D,过点P作PE⊥AC于点E.