题目内容
11.计算:(1)解方程:2(1-2x)2=162;
(2)化简:$\sqrt{\frac{1}{7}}$×(-$\sqrt{28}$)+$\root{3}{{8}^{2}}$+$\sqrt{{3}^{-2}}$;
(3)化简:|3-π|+$\sqrt{(1-\sqrt{2})^{2}}$+$\sqrt{16}$.
分析 (1)方程整理后,利用平方根定义开方即可求出解;
(2)原式利用平方根、立方根定义,以及负整数指数幂法则计算即可得到结果;
(3)原式利用绝对值的代数意义,二次根式性质,以及算术平方根定义计算即可得到结果.
解答 解:(1)方程整理得:(1-2x)2=81,
开方得:1-2x=9或1-2x=-9,
解得:x=-4或x=5;
(2)原式=$\frac{\sqrt{7}}{7}$×(-2$\sqrt{7}$)+4+$\frac{1}{3}$=2$\frac{1}{3}$;
(3)原式=π-3+$\sqrt{2}$-1+4=π+$\sqrt{2}$.
点评 此题考查了实数的运算,以及负整数指数幂,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
1.要得到y=(x-3)2-2的图象,只要将y=x2的图象( )
| A. | 由向左平移3个单位,再向上平移2个单位 | |
| B. | 由向右平移3个单位,再向下平移2个单位 | |
| C. | 由向右平移3个单位,再向上平移2个单位 | |
| D. | 由向左平移3个单位,再向下平移2个单位 |
19.若|x|=-x,则x的取值范围是( )
| A. | x=-1 | B. | x<0 | C. | x≥0 | D. | x≤0 |
20.函数y=$\sqrt{x+2}$中,自变量x的取值范围是( )
| A. | x>2 | B. | x≥-2 | C. | x≤-2 | D. | x>-2 |
1.某商品标价为a,若降价10%后出售,则实际售价为( )
| A. | 1.1a | B. | a | C. | 0.99a | D. | 0.9a |
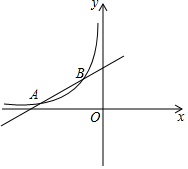 如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?
如图,已知A(-4,$\frac{1}{2}$),B(-1,2)是一次函数y=kx+b与反比例函数y=$\frac{m}{x}$(m<0)图象的两个交点,求反比例函数的解析式,并根据图象直接回答:在第二象限内,当x取何值时,一次函数的值大于反比例函数的值?