题目内容
6.先化简,再计算:($\frac{{x}^{2}}{x+1}$-x+1)÷$\frac{x}{{x}^{2}-1}$,请从0,1,-1,$\sqrt{3}$选择一个恰当的数,作为x的值,代入求值.分析 先把括号内通分,再把除法运算化为乘法运算,然后约分得到原式=$\frac{x-1}{x}$,再利用分式有意义的条件得到x只能取$\sqrt{3}$,于是把x=$\sqrt{3}$代入计算即可.
解答 解:原式=[$\frac{{x}^{2}}{x+1}$-$\frac{(x-1)(x+1)}{x+1}$]•$\frac{(x+1)(x-1)}{x}$
=$\frac{1}{x+1}$•$\frac{(x+1)(x-1)}{x}$
=$\frac{x-1}{x}$,
当x=$\sqrt{3}$时,原式=$\frac{\sqrt{3}-1}{\sqrt{3}}$=1-$\frac{\sqrt{3}}{3}$.
点评 本题考查了分式的化简求值:先把分式化简后,再把分式中未知数对应的值代入求出分式的值.在化简的过程中要注意运算顺序和分式的化简.化简的最后结果分子、分母要进行约分,注意运算的结果要化成最简分式或整式.

练习册系列答案
相关题目
1. 如图,在平行四边形ABCD,∠B=70°,AE平分∠BAD交BC与点E,CF∥AE交AD于点F,则∠BCF的度数是( )
如图,在平行四边形ABCD,∠B=70°,AE平分∠BAD交BC与点E,CF∥AE交AD于点F,则∠BCF的度数是( )
 如图,在平行四边形ABCD,∠B=70°,AE平分∠BAD交BC与点E,CF∥AE交AD于点F,则∠BCF的度数是( )
如图,在平行四边形ABCD,∠B=70°,AE平分∠BAD交BC与点E,CF∥AE交AD于点F,则∠BCF的度数是( )| A. | 45° | B. | 55° | C. | 65° | D. | 75° |
15.要了解某校1500名学生的课外作业负担情况,你认为以下抽样方法中比较合理的是( )
| A. | 调查全体女生 | B. | 调查全体男生 | ||
| C. | 调查九年级全体学生 | D. | 调查七、八、九年级各100名学生 |
16.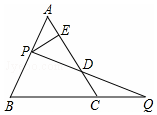 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
 如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )
如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线一点,当PA=CQ时,连结PQ交AC于D,则DE的长为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
 如图,已知AB=DE,BE=CF,AC=DF,求证:AB∥DE.
如图,已知AB=DE,BE=CF,AC=DF,求证:AB∥DE.