题目内容
2.设$\frac{4x-9}{3{x}^{2}-x-2}$=$\frac{A}{3x+2}$-$\frac{B}{x-1}$(A、B为常数),求A、B的值.分析 先把等式右边的分式通分,再令等式两边的分子相等即可得出A、B的值.
解答 解:右边=$\frac{A(x-1)-B(3x+2)}{(3x+2)(x-1)}$=$\frac{(A-3B)x-(A+2B)}{3{x}^{2}-x-2}$,
∵分式两边的等式相等,
∴4x-9=(A-3B)x-(A+2B),
∴$\left\{\begin{array}{l}{A-3B=4}\\{A+2B=9}\end{array}\right.$,
解得$\left\{\begin{array}{l}{A=7}\\{B=1}\end{array}\right.$.
点评 本题考查的是分式的加减法,在解答此题问题时要注意通分的灵活应用.

练习册系列答案
相关题目
12. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
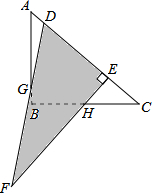 一副三角尺按如图所示方式放置,试求∠AGF的度数.
一副三角尺按如图所示方式放置,试求∠AGF的度数.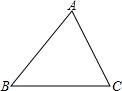 如图,在△ABC中,画出它们的三条中线AD、BE、CF,三条中线交于一点G,AG与GD的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立?
如图,在△ABC中,画出它们的三条中线AD、BE、CF,三条中线交于一点G,AG与GD的长度有什么关系?用刻度尺验证你的结论,换一个三角形试试看,上述结论是否还成立? 如图,P是△ABC内一点,试说明2(PA+PB+PC)>(AB+BC+AC)
如图,P是△ABC内一点,试说明2(PA+PB+PC)>(AB+BC+AC)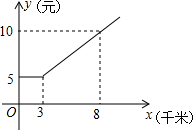 某歌唱大赛已经拉开序幕,欢欢准备乘坐出租车去比赛现场观看比赛,如图是乘坐出租车费用y(元)与路程x(千米)之间的函数图象.
某歌唱大赛已经拉开序幕,欢欢准备乘坐出租车去比赛现场观看比赛,如图是乘坐出租车费用y(元)与路程x(千米)之间的函数图象.