题目内容
10.在平面直角坐标系xOy中,抛物线y=mx2-2mx-3(m≠0)与x轴交于A(3,0),B两点.(1)求抛物线的表达式及点B的坐标;
(2)当-2<x<3时的函数图象记为G,求此时函数y的取值范围;
(3)在(2)的条件下,将图象G在x轴上方的部分沿x轴翻折,图象G的其余部分保持不变,得到一个新图象M.若经过点C(4.2)的直线y=kx+b(k≠0)与图象M在第三象限内有两个公共点,结合图象求b的取值范围.
分析 (1)把点A的坐标代入抛物线解析式,列出关于m的方程,通过解该方程可以求得m的值;
(2)根据抛物线解析式求得对称轴,所以由抛物线的对称性和增减性进行解答;
(3)根据题意作出函数图象,由图象直接回答问题.
解答  解:(1)将A(3,0)代入,得m=1.
解:(1)将A(3,0)代入,得m=1.
∴抛物线的表达式为y=x2-2x-3.
B点的坐标(-1,0).
(2)y=x2-2x-3=(x-1)2-4.
∵当-2<x<1时,y随x增大而减小;
当1≤x<3时,y随x增大而增大,
∴当x=1,y最小=-4.
当x=-2,y=5.
∴y的取值范围是-4≤y<5.
(3)当直线y=kx+b经过B(-1,0)和点(4,2)时,
解析式为y=$\frac{2}{5}$x+$\frac{2}{5}$.
当直线y=kx+b经过(-2,-5)和点(4,2)时,
解析式为y=$\frac{7}{6}$x-$\frac{8}{3}$.
结合图象可得,b的取值范围是-$\frac{8}{3}$<b<$\frac{2}{5}$.
点评 本题考查了二次函数图象与几何变换,待定系数法求二次函数的解析式.解题时,注意数形结合,使抽象的问题变得具体化,降低了解题的难度.

练习册系列答案
相关题目
1.在平面直角坐标系中将点P(2,-3)向上平移4个单位后得到点Q,则点Q的坐标是( )
| A. | (2,1) | B. | (2,-7) | C. | (6,-3) | D. | (-2,-3) |
15.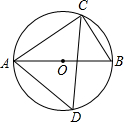 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
 如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )
如图,AB是⊙O的直径,若∠ADC=55°,则∠BAC的大小是( )| A. | 35° | B. | 55° | C. | 70° | D. | 110° |
19.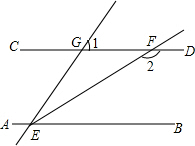 如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )
如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )
 如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )
如图,已知直线AB∥CD,∠BEG的平分线EF交CD于点F,若∠1=42°,则∠2等于( )| A. | 159° | B. | 148° | C. | 142° | D. | 138° |
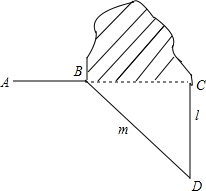 小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?
小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?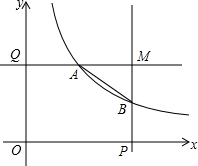 如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.
如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点. 在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.
在平面直角坐标系xOy中,二次函数y=(a-1)x2+2x+1与x轴有交点,a为正整数.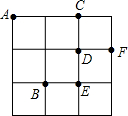 在3×3的方格中,A、B、C、D、E、F分别位于如图所示的小正方形的顶点上,从C、D、E、F四点中任意取一点,以所取得一点及点A、B为顶点画三角形,则所画三角形为等腰三角形的概率是$\frac{3}{4}$.
在3×3的方格中,A、B、C、D、E、F分别位于如图所示的小正方形的顶点上,从C、D、E、F四点中任意取一点,以所取得一点及点A、B为顶点画三角形,则所画三角形为等腰三角形的概率是$\frac{3}{4}$.